proszę o rozwiązanie anna: w trójkącie ABC punkty D i E są środkami boków AC i BC a punkt F środkiem odcinka DC Wiedząc że ∡EDC = 45⁰ ∡ FED = 30⁰ oraz I FE I = 8 oblicz pole czworokąta ABEF odp P = 56(1 + √3)

chichi: Wytłumacz nam proszę, jak to możliwe, że jedyne zadania, które wrzucasz przez dlugi okres to planimetria. Zadania te są zazwyczaj banalne, a Ty i tak niczego się nie uczysz z naszych rozwiązań. Jaki jest zatem sens aby ktokolwiek je robił?

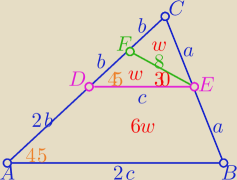
Eta: w −− pole 2w=P_ΔDEC ΔABC∼ΔDEC w skali k=2 to P_ABEF= 7w Z tw. sinusów w ΔDEF oblicz b .... (b=4√2 i z tw. cosinusów wΔDEF oblicz c, c>8 otrzymasz c=4+4√3

	1
w=		*b*c*sin45o = ......... = 2c
	2

P_ABEF= 14 c= ......= 56(√3+1) ======================== @anna .... analizuj i ucz się Powodzenia

anna: dziękuję bardzo

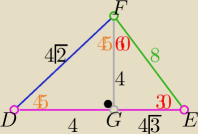
Eta: Można jeszcze tak: W ΔDEF skorzystać z dwóch trójkątów "ekierkowych" i mamy P_DEF=w=8(√3+1) to P_ABEF=7w=56(√3+1) ==================