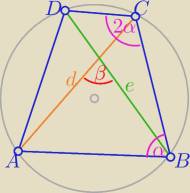
Proszę o rozwiązanie krok po kroku kot: W okrąg o promieniu R wpisano czworokąt ABCD, którego przekątna AC ma długość d, kąt DCB jest dwa razy większy od kąta ABC i przekątne przecinają się pod kątem o mierze ^π₂− |∠ABC|. Oblicz pole tego czworokąta.

Eta:

	1		1		π
PABCD−		*d*e*sinβ =		decosα , bo sinβ=sin(		−α)=cosα
	2		2		2

z tw. sinusów w ΔABC i w ΔBCD

	d
sinα=		f=2R*sin(2α)= 2R*2sinα*cosα = 2dcosα
	2R

	d2
cos2α= 1−
	4R2

to P=d²cos²α =.................. dokończ