Dwa boki równoległoboku zawierają się w prostych o równaniach Hans: Dwa boki równoległoboku zawierają się w prostych o równaniach

	1
AB: y=		x−2, AD: y=2x − 5.
	2

Środek symetrii równoległoboku ma współrzędne S= (5,2). Wyznacz współrzędne wierzchołka B tego równoległoboku

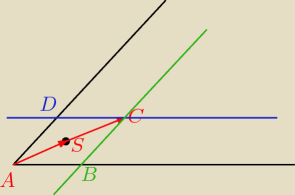
Basia: schemat rozwiązania: 1. szukasz punktu A (układ równań pr.AB i pr.AD 2. szukasz punktu C (AS^→=SC^→) 3. piszesz równanie pr.BC || pr.AD i przechodzącej przez C 4. znajdujesz B (układ równań pr.AB i pr.BC)

Tysia1992: y=1/2x−2 Klamerka y=2x−5 1/2x−2=3x−5 1/2−2x=−5+2 −1,5x=−3 I:(−1.5) x=2 y=1/2*2−2 y=−1 A=(2,−1) C=(p, r) Punkt S− środek odcinka AC: (5,2)=(2+p/2;−1+r/2) 2+p/2=5 klamerka r−1/2=2 p=8 r=5 C=(8,5) Prosta BC jest równoległa do prostej AD i przechodzi przez punkt C: y=2x+k 5=2*8+k k=−11 BC:y=2x−11 Punkt B jest punktem wspólnym prostych AB i BC: y=1/2x−2 klamerka y=2x−11 1/2x−2=2x−11 3/2x=9 x=2*6−11 y=1 B=(6,1) Posty: 9214 Dołączenie: 10 Paź 2009, 19:08 Płeć: Otrzymane podziękowania: 2769

MYCHA: liczba x przy dzieleniu przez 5 daje reszte 3.liczbe x mozna wiec w postaci(n∊N): A.3n+5 B.5n+3 C.5(n+3) D.3(n+5)