proszę o rozwiązanie anna: w trapezie ABCD kąty BAD i ADC są proste Dwusieczne kątów CBA i DCB przecinają się w punkcie E który należy do boku AD a) wykaż że trójkąty ABE EBC i DEC są podobne b) Wiedząc dodatkowo że AB = 12 , AE = 9 oblicz długość podstawy DC

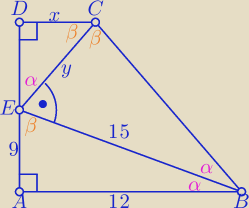
chichi: 2α + 2β = 180^o ⇒ α + β = 90^o ⇒ |∡BEC| = 90^o ΔABE ∼ ΔEBC ∼ ΔDEC (cecha k−k−k)

	9		y		45
|EB| = √92 + 122 = 15, zatem:		=		⇒ y =		(z pod. ΔBAE i ΔBEC)
	12		15		4

15		45     4		27
	=		⇒ x =		(z pod. ΔBAE i ΔEDC)
9		x		4

anna: dziękuję bardzo

Eta: Prawie bez obliczeń

	3
trójkaty podobne w skali k=
	4

	3		27
to x= |DC|=9*		=
	4		4

================ i po ptokach