Geometria analityczna yn: Wyznacz równanie ogólne prostej przechodzącej przez punkt przecięcia prostych x – y = 1 i 2x + y = 8 i odległej od początku układu współrzędnych o ⁶₅

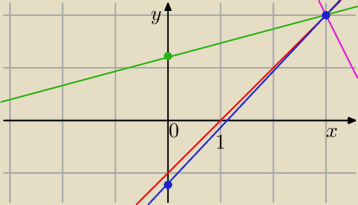
janek191: y = ax + b 2 = 3 a + b ⇒ b = 2 − 3 a y = a x − 3 a + 2 a x − y −3 a + 2 = 0 O = (0,0)

I 0 − 0 − 3 a + 2 I		6
	=
√a2 + 1		5

I −3 a + 2 I *5 = 6 I − 15 a + 10 I = 6 − 15 a + 10 = − 6 lub − 15 a + 10 = 6 − 15 a = − 16

	16		4
a =		lub a =
	15		15

więc

	6		6
b = −		lub b =
	5		5

zatem

	16		6		4		6
y =		x −		lub y =		x +
	15		5		15		5

====================================

janek191: Dokończ

maturka: A co się stało z √a²+1 ?

chichi: Źle rozwiązałeś równanie, co stało się z √a² + 1?

maturka:

chichi: Mnie wyszło:

	4		16		26
y =		x − 2 ∨ y =		x +
	3		63		21

Autor zechce przekształcić równania prostych do postaci ogólnej i będzie wynik

janek191: Zgubiłem. Zaćmienie umysłu

yn:

	16		26		4
0 =		x − y +		v 0 =		x − y − 2
	63		21		3

Czyli to jest już gotowa odpowiedź i nie musimy odrzucać jednego równania?

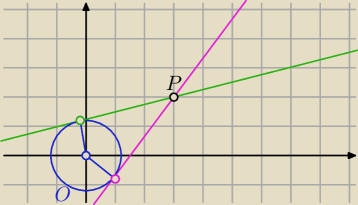
chichi: Może nieco dłuższy sposób, ale równie ciekawy: Niech: k: x − y =1 ∧ m: 2x + y = 8 ⇒ k ∩ m = P = (3,2)

	6
Zaczepiam okrąg o środku w punkcie (0,0) i promieniu długości równej		:
	5

	36
O : x2 + y2 =
	25

Równanie prostej przechodząca przez punkt P: n: y = ax + b ∧ P ∊ n ⇒ b = 2 − 3a ⇒ y = ax + 2 − 3a Szukane proste, to styczne do okręgu O przechodzące przez punkt P, tworzę układ równań:

⎧	x2 + y2 = 36/25
⎨
⎩	y = ax + 2 − 3a

	64
(**) x2 + (ax + 2 − 3a)2 = 1.44 ⇔ (a2 + 1)x2 + (4a − 6a2)x + 9a2 − 12a +		= 0
	25

Równanie będzie posiadało 1 rozwiązanie wtw. gdy Δ = 0, zatem:

	64
(4a − 6a2)2 − 4(a2 + 1)(9a2 − 12a +		) = 0 ⇔
	25

	16		4
⇔ 189a2 − 300a + 64 = 0 ⇔ (3a − 4)(63a − 16) = 0 ⇔ a ∊ {		,		}
	63		3

No i pozostało wyznaczyć równania prostych i przekształcić do postaci ogólnej, o godz. 20:58 podałem prawidłowe równania szukanych prostych. Rzecz jasna rozwiązywać polecam w sposób zaproponowany przez @janek191, ale warto też czasami poeksperymentować i poszukać różnych rozwiązań, te najkrótsze są oczywiście najlepsze