Zadania dla @Mila
chichi:
W czworokącie ABCD, przekątne AC i BD przecinają się w punkcie S takim, że |AS|=|SC| oraz
|SD|=2|SB|. Punkty E i F leżą odpowiednio na odcinkach SC i BC, tak że
| | |AC| | | |BF| | |
|
| = |
| . Pokaż, że punkty E, F i D są współliniowe. |
| | |SE| | | |FC| | |
16 lut 17:15
chichi:
W poleceniu brakło jednej równości, mianowicie:
16 lut 17:16
Mila:
Dziękuję.
16 lut 17:19
chichi:
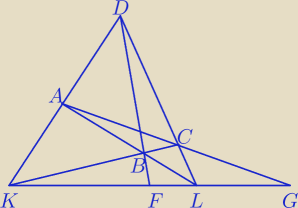
Dany jest czworokąt wypukły ABCD. Niech K będzie punktem przecięcia się prostych AC i BD, L −
punktem przecięcia prostych AB i CD, G − punktem przecięcia prostych AC i KL oraz F − punktem
| | |KF| | | |KG| | |
przecięcia prostych BD i KL. Pokaż, że |
| = |
| . |
| | |FL| | | |GL| | |
Naniosłem Ci wszystko na rysunek
16 lut 17:27
chichi:
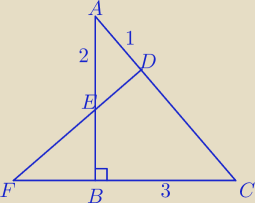
Na przedstawionym rysunku trójkąt ABC jest prostokątny (|∡ABC| = 90
o) a długości boków AB oraz
BC wynoszą odpowiednio 4cm i 3cm. Punkt D należy do boku AC w taki sposób, że |AD| = 1cm.
Pondato punkt E jest środkiem boku AB. Proste ED i BC przecinają się w punkcie F.
Znajdź długość odcinka BF.
16 lut 17:34
chichi:
Punkty A', B' oraz C' leżą odpowiednio na bokach BC, AC, oraz AB trójkąta ABC i dzielą je
odpowiednio w stosunkach:
| |A'B| | | |B'C| | | |C'A| | |
| = ϱ, |
| = λ, |
| = μ. |
| |A'C| | | |B'A| | | |C'B| | |
Punkt D jest punktem przecięcia się prostych AA' oraz B'C'. Pokaż, że zachodzą równości:
| |DC'| | | ϱμ(1 − λ) | | |DA| | | μ(ϱ − 1) | |
| = |
| oraz |
| = |
| . |
| |DB'| | | μ − 1 | | |DA'| | | ϱλμ − 1 | |
16 lut 17:52
chichi:
Daj znać, gdy będzie potrzeba więcej. Te są "nawet" ciekawe
16 lut 17:53
Mila:
Dziękuję, czytam
16 lut 18:00
Mila:
17:27 niezgodność treści z rysunkiem, ale poprawiłam u siebie.
16 lut 18:47
chichi:
Tak winno być K = AD ∩ BC, dziękuję
16 lut 19:33
Kacper:
chichi skąd te zadanka?
17 lut 17:32
17 lut 17:45
chichi:
Te zadania pochodzą z zagranicznych podręczników przygotowujących do olimpiad matematycznych,
są zebrane z wielu krajów. Jeśli są również w linkach podanych przez @
Mila to właśnie
stamtąd zostały buchnięte
17 lut 18:21
Kacper:
Podziwiam za wiedzę i upór w nauce
17 lut 20:09