Ekstrema funkcji 1988: Wyznacz ekstrema funkcji f(x) = sin²x + cosx f'(x) = sinx(2cox−1) sinx = 0 v cosx = −¹₂

	π		π
x = kπ v x = −		+2kπ v x =		+2kπ
	3		3

Nie wiem, jak dalej sobie z tym fantem poradzić

Maciess: Policz drugą pochodną i zbadaj jej znak w punktach podejrzanych

I'm back: Albo − sprawdzasz wartość w dwuch punktach (np x=0 i x=π/3) i na podstawie tego wiesz jaka monotonicznosc funkcja miała w tym przedziale, a na podstawie tego jesteś w stanie narysować 'wezyka' pochodnej i wskazać przedziały monotonicznosci tejże funkcji

I'm back: W dwóch miało być

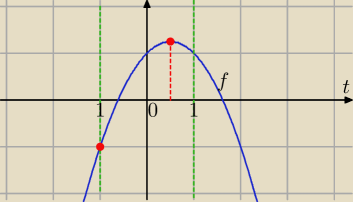
Mila: sin²x=1−cos²x f(x)=−cos²x+cosx+1 1) cosx=t f(t)=−t²+t+1

	1
tw=
	2

	1		5		5		1
f(		)=		największa wartość f(t)=		dla t=		⇔
	2		4		4		2

	1		π
cosx=		dla x=±		+2kπ funkcja f(x) maksima lokalne
	2		3

f(t) =f(−1)=−1 najmniejsza wartość f(t) dla t=−1⇔ cosx=−1 dla x=π+2kπ , k∊C funkcja f(x) ma minima lokalne