Liczby zespolone Damian#UDM: 1. Oblicz pierwiastki liczby zespolonej z=³√(2−i)⁶ 2. Rozwiąż równanie w zbiorze liczb zespolonych [z+i]=z−i gdzie [] oznaczana sprzężenie. 3. Na płaszczyźnie zespolonej narysuj zbiory liczb "z" spełniających podane warunki: a) Re(iz+2)≥0 b) Im(z²)<0 c) [z−i]=z−1 d) |z−3+4i|=1 e) 2≤|iz−5|<3

	z+i
f) |		|≥1
	z2+1

g) Arg(z+2−i)=π h) ²₃π≤Arg(3i−z)≤⁵₆π

janek191: z.2 z = x + i y Mamy −−−−−−− x + i y +i = x + i y − i −−−−−−− x + (y +1) i = x + ( y − 1) i x − ( y + 1) i = x + ( y − 1) i − y − 1 = y − 1 2 y = 0 y = 0 z = x + 0 i ========

Damian#UDM: 4. Korzystając ze wzoru de Moivre'a wyraź sin(3x) przez sin(x).

janek191: Z wzoru mamy: ( cos x + i sin x)³ = cos 3x + i sin 3x L = cos³ x − 3 sin² x*cos x + 3 i *sin x*cos² x − i sin³ x = = ( cos³ x − 3 sin² x*cos x ) + i sin x*( 3 cos² x − sin² x) zatem po porównaniu części urojonych mamy : sin x*( 3 cos² x − sin² x) = sin 3x sin x *( 3*(1 − sin² x) − sin² x] = sin 3x sin x*( 3 4 sin² x) = sin 3 x 3 sin x − 4 sin³ x = sin 3x sin 3 x = 3 sin x − 4 sin³ x =====================

Mila: z=³√(2−i)⁶ z=³√[(2−i)²]³ z=³√(3−4i)³ z³=(3−4i)³ z³−(3−4i)³=0 (z−3+4i)=0 lub (z²+(3−4i) z+(3−4i)²)=0 z=3−4i lub Δ=(3−4i)²−4*(3−4i)²=−3(3−4i)²=3i²*(3−4i)² dokończ

Damian#UDM: Ludzie, bardzo dziękuje wam z tym 1. nie pomyślałbym, żeby do potęgi trzeciej podnieść, a teraz będę wiedział Proszę jeszcze z 3. na pewno c, e, f i h

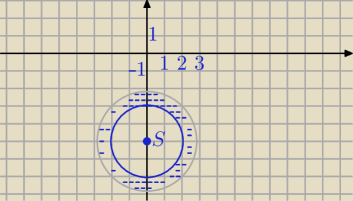
Mila: e) 2≤|iz−5|<3 2≤|iz+i²*5|<3 2≤|i|*|z+5i|<3⇔ 2≤|z−(−5i)|<3 pierścień, bez punktów na okręgu o r=3 środek pierścienia S=(0,−5)

Mila: f) z²+1=z²−i² z≠i i z≠−i

	z+i
|		|≥1 ⇔
	z2+1

|z+i|≥|z²+1|⇔ |z+i|≥|z²−i²| |z+i|−|z−i|*|z+i|≥0 |z+i|*(1−|z−i|)≥0 dalej sam

Damian#UDM: Super, kolejna zależność |i|=1, o tym nie wiedziałem

Damian#UDM: Czy są jeszcze jakieś zależności, które mogą być przydatne?

	z−
Na pewno wiem, że mnożenie razy		sprzężenie jest bardzo przydatne
	z−

ite: janek w zad.2 (9:03) po lewej stronie równości ma być sprzężenie: (z+i)*=z−i więc inne rozwiązanie i wynik

janek191: z = x + i y Lewa strona równania −−−− −−−−−−−− −−−−−−−−− z + i = ( x + i y) + i = x + i*( y + 1) = x − i *(y + 1) Prawa strona równania z − i = x + i y − i = x + i*( y − 1) Co jest źle?

Mila: Janek ma dobrze.

Damian#UDM: Dopytam jeszcze czy znacie jakieś zależności lub triki, które mogłyby przydać się przy rozwiązywaniu zadań z liczb zespolonych?

Kacper: Chodzić na wykłady i zadać to pytanie wykładowcy warto 😊

luui: i² = −1 −1/1 = 1/−1 √−1/1 = √1/−1 √−1/√1 = √1/√−1 i/1 = 1/i i² = 1 −1 = 1 Coś poszło nie tak...

Damian#UDM: Dziękuję Wam za pomoc. Sam to spróbuję ogarnąć

ite: Mila, janek nie zauważyłam, że tylko podwójny rząd kresek jest podkreśleniem, a pojedynczy oznacza sprzężenie. Więc moja uwaga nie była potrzebna.