Bardzo proszę o pomoc
janko: Określ liczbę rozwiązań równania | |x−3| − 2| − 4 = m w zależności d parametru m
13 lut 22:24
kerajs:
Sugeruję zrobić wykres lewej strony, i wynik odczytać z wykresu
Brak rozwiązania dla m<−4
2 rozwiązania dla m= −4 lub m > −2
3 rozwiązania dla m= −2
4 rozwiązania dla −4 < m < −2
13 lut 22:30
mydlix:
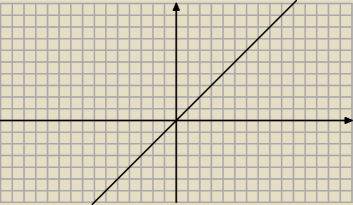
Pierw rysujesz y=x
14 lut 08:42
mydlix:
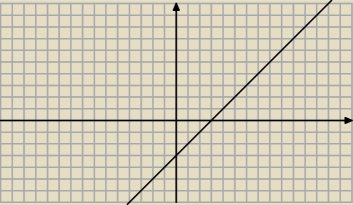
Następnie y=x−3 (wykres y=x obniżony o trzy kratki w dół, mówiąc nieformalnie, a formalnie
przesunięty o wektor u=[0,−3])
14 lut 08:44
mydlix:
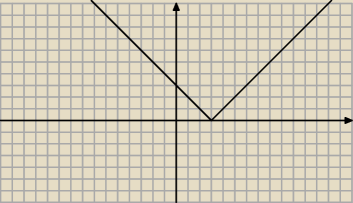
Teraz mamy y=|x−3|, czyli dajemy wartość bezwzględną, czyli wszystko co jest pod osią OX
odbijamy symetrycznie względem tej osi
14 lut 08:45
mydlix:
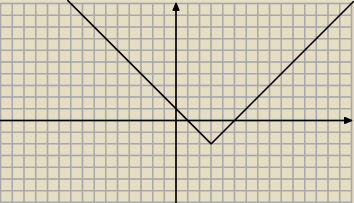
Następnie mamy y=|x−3|−2, czyli obniżamy o dwie kratki (o wektor u=[0,−2])
14 lut 08:47
mydlix:
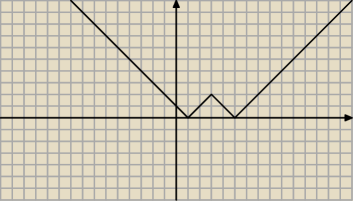
Teraz znowu wartość bezwzględna, czyli odbijamy wszystko, co jest poniżej osi OX względem tej
osi i będziemy mieli: ||x−3| − 2||
14 lut 08:50
mydlix:
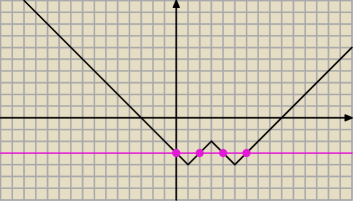
Teraz wszystko obniżamy o cztery kratki (wektor u=[0,−4]) i mamy y=||x−3| − 2||−4
Liczbą rozwiązań równania ||x−3| − 2||−4=m będzie liczba punktów przecięcia prostej y=m i
wykresem y=||x−3| − 2||−4, np. dla m=−3 mamy 4 punkty przecięcia, czyli cztery rozwiązania
(patrz rysunek)
Teraz odczytujemy, że:
|ZR|=0 dla m∊(−
∞;−4)
|ZR|=2 dla m∊{−4}∪(−2;+
∞)
|ZR|=3 dla m=−2
|ZR|=4 dla m∊(−4;−2)
14 lut 08:57
janko: Bardzo dziękuję za wyczerpującą odpowiedź.
14 lut 22:07
 Pierw rysujesz y=x
Pierw rysujesz y=x
 Następnie y=x−3 (wykres y=x obniżony o trzy kratki w dół, mówiąc nieformalnie, a formalnie
przesunięty o wektor u=[0,−3])
Następnie y=x−3 (wykres y=x obniżony o trzy kratki w dół, mówiąc nieformalnie, a formalnie
przesunięty o wektor u=[0,−3])
 Teraz mamy y=|x−3|, czyli dajemy wartość bezwzględną, czyli wszystko co jest pod osią OX
odbijamy symetrycznie względem tej osi
Teraz mamy y=|x−3|, czyli dajemy wartość bezwzględną, czyli wszystko co jest pod osią OX
odbijamy symetrycznie względem tej osi
 Następnie mamy y=|x−3|−2, czyli obniżamy o dwie kratki (o wektor u=[0,−2])
Następnie mamy y=|x−3|−2, czyli obniżamy o dwie kratki (o wektor u=[0,−2])
 Teraz znowu wartość bezwzględna, czyli odbijamy wszystko, co jest poniżej osi OX względem tej
osi i będziemy mieli: ||x−3| − 2||
Teraz znowu wartość bezwzględna, czyli odbijamy wszystko, co jest poniżej osi OX względem tej
osi i będziemy mieli: ||x−3| − 2||
 Teraz wszystko obniżamy o cztery kratki (wektor u=[0,−4]) i mamy y=||x−3| − 2||−4
Liczbą rozwiązań równania ||x−3| − 2||−4=m będzie liczba punktów przecięcia prostej y=m i
wykresem y=||x−3| − 2||−4, np. dla m=−3 mamy 4 punkty przecięcia, czyli cztery rozwiązania
(patrz rysunek)
Teraz odczytujemy, że:
|ZR|=0 dla m∊(−∞;−4)
|ZR|=2 dla m∊{−4}∪(−2;+∞)
|ZR|=3 dla m=−2
|ZR|=4 dla m∊(−4;−2)
Teraz wszystko obniżamy o cztery kratki (wektor u=[0,−4]) i mamy y=||x−3| − 2||−4
Liczbą rozwiązań równania ||x−3| − 2||−4=m będzie liczba punktów przecięcia prostej y=m i
wykresem y=||x−3| − 2||−4, np. dla m=−3 mamy 4 punkty przecięcia, czyli cztery rozwiązania
(patrz rysunek)
Teraz odczytujemy, że:
|ZR|=0 dla m∊(−∞;−4)
|ZR|=2 dla m∊{−4}∪(−2;+∞)
|ZR|=3 dla m=−2
|ZR|=4 dla m∊(−4;−2)