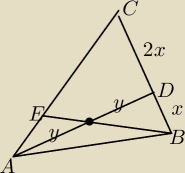
Matura rozszerzona, planimetria trójkąt Luke: W trójkącie ostrokątnym ABC punkt D dzieli bok BC w stosunku 1:2 licząc od wierzchołka B . Z wierzchołka B poprowadzono prostą przechodzącą przez środek odcinka AD , która przecięła bok AC w punkcie E. Oblicz, w jakiej proporcji, licząc od wierzchołka A , punkt E dzieli bok AC . Zrobiłem, ale nie wiem od czego zacząć. Będę wdzięczny za wskazówkę

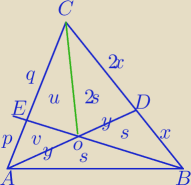Mila: 1)CO − środkowa ΔADC⇔pola: v+u=2s P_ΔABC=6s

p		v
	=		− Δmają tę samą wysokość
q		u

v+s		p		v
	=		=
u+3s		q		u

dokończysz?

Mila: II sposób

AE		BC		DO
	*		*		=1
EC		CD		OA

AE		3x
	*		*1=1
EC		x

AE		1
	=
EC		3

Euler: Twierdzenie Menelaosa, nice