nierówność z wartością bezwzględną niewiem: Czy tak można rozpisać? |x|<x+2 x<x+2 ⋀ x>−x−2 0<2 ⋀ 2x>−2 x∊R ⋀ x>−1 x∊(−1, +∞) Wynik jest prawidłowy, ale nie wiem czy tak wolno

I'm back: Brakuje mi w drugiej linijce informacje odnośnie przypadków

I'm back: I wtedy nie mamy 'i' tylko 'lub' pomiędzy nierównościami

niewiem: Dlaczego lub? skoro jest mniejsze?

wredulus_pospolitus: 'lub' w połączeniu z warunkami by były użyte. Zapis który zrobiiłeś/−aś nie jest niepoprawny, jednak jest nieprecyzyjny (w wielu nierównościach doprowadziłby do błędnej odpowiedzi) i trzeba o tym pamiętać. Jeżeli dopiero zaczynasz w szkole 'zabawę' z wartością bezwzględną, rób tak jak nauczyciel przekazał.

chichi: Nie wolno.

niewiem: wredulus, pokaż przykład, w którym to prowadzi do błędnej odpowiedzi? wszystkie przykłady, które liczę w ten sposób zgadzają się z odpowiedziami. chichi a jakieś wytłumaczenie dlaczego nie wolno?

wredulus_pospolitus: przykład:

	1
|		| < 2 −−−> powinno wyjść (−∞ ; −1/2) u (1/2 , +∞)
	x

pokaż jak Ci to wyjdzie nie mówiąc już o tym, że przy samym rozwiązywaniu napotykasz na problem w momencie mnożenia przez 'x'

niewiem: D=R−{0}

1		1
	<2 ∧		>−2
x		x

Mnożę obie nierówności stronami przez x² x<2x² ∧ x>−2x² 2x²−x>0 ∧ 2x²+x>0 x(2x−1)>0 ∧ x(2x+1)>0 x∊(−∞,0)∪(1/2, +∞) ∧ x∊(−∞,−1/2)∪(0, +∞) Ostatecznie x∊(−∞,−1/2)∪(1/2, +∞), zgadza się z tym co podałeś.

niewiem: chodzi mi o to, że w szkole uczono mnie, że jak mamy |x|<liczba (liczba>=0), to możemy sobie rozpisać na coś takiego |x|<3 x<3 ∧ x>−3 A jak było |x| < x , to kazali rozbijać na przypadki (1 dla x>=0; 2 dla x<0) a ja bym chciała to zrobić tak samo jak tamto wyżej, czyli: |x| < x x < x ∧ x>−x

niewiem: pomóżcie, bo chciałabym wiedzieć gdzie jest błąd w moim rozumowaniu

niewiem:

niewiem: Może Mila lub Eta pomożecie? widzę, że dużo tutaj piszecie

chichi: Pominę sobie nierówność i pokaże Ci to na przykładzie równania: Wg. Ciebie:

	8
|x + 2| = 2x + 6 ⇔ x + 2 = 2x + 6 ∨ x + 2 = −2x − 6 ⇔ x ∊ {−4, −		}
	3

Ten wynik nie jest oczywiście prawdziwy... Winno być: dziedzina równania: 2x + 6 ≥ 0 ⇔ x ∊ [−3, +∞) i tutaj widać, że (−4) się nie załapie, to samo otrzymamy rozwiązując w ten szkolny sposób, rozpisując na 2 przypadki, czyli w tym przypadku: (1^o) dla x < −2 mamy |x + 2| = −x − 2 (2^o) dla x ≥ −2 mamy |x + 2| = x + 2 i dalej jedziemy tym szkolnym schemacikiem

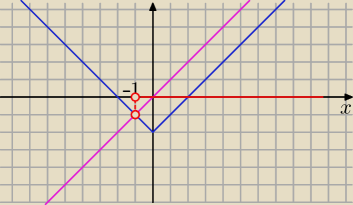
Eta: graficznie |x|−2<x y=|x|−2| y=x x∊(−1,∞) ========

Eta: Algebraicznie x+2≥0 ⇒ x≥ −2 x<x+2 ⋀ x>−x−2 0<2 ⋀ 2x>−2 ⋀ x≥ −2 Odp: x∊(−1,∞) ==========

kerajs: ''niewiem: Czy tak można rozpisać?'' Tak, lecz przed opuszczeniem wartości bezwzględnej musisz zrobić założenie o nieujemności prawej strony. Sposób z założeniami znaku wyrażenia w wartości bezwzględnej jest bardziej uniwersalny i dlatego preferowany w szkole.

niewiem: chichi, wiem, że w równaniach tak nie wolno Dziękuję, za wszystkie odpowiedzi

chichi: No własnie widzę jak wiesz... A nierówność to co? Określasz dziedzinę tak samo jak to pokazałem w przypadku równania...

mydlix: Wartość bezwzględna ma własność, że jeśli a>0, to IxI<a wtedy i tylko wtedy, gdy −a<x<a, ale wtedy gdy a jest jakąś liczbą, a nie zmienną. Zatem jeśli rozpisujesz IxI<3 to możesz zastosować −3<x<3, bo 3 jest liczbą, ale jeśli IxI<x, to nie, bo x jest zmienną, musisz rozpisać przypadki i określić założenia

mydlix: Poza tym musisz się przyzwyczaić do rozpisywania przypadków, bo jeśli jesteś na rozszerzeniu, to niedługo czeka Cię, np: Ix−3I−Ix+4I<1