równoległobok KM: W równoległoboku ABCD punkt M jest środkiem boku AB, a S jest punktem na boku BC. Jeśli O= AS ∩ DM i P_ABCD = 20P_AOM, udowodnij, że punkt S jest środkiem boku BC.

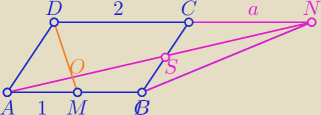
chichi: Ojj coś brak chętnych na forum...

1		1
	=		⇒ a = 2 ⇒ S = SBC □
4(a + 3)		20

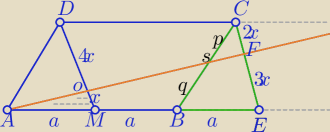
Mila: 1) CE|| DM, |CE|=|DM|

	1		1
2) PΔAMD=		P , PΔAOM=		P
	4		20

	4		OP
PΔAOD=		P⇒		=4:1
	20		OM

3)

	FE		1x
ΔAEF∼AMO ⇔		=
	3a		a

|FE|=3x, |CF|=2x 4) ΔBEC i prosta AF− tw. Menelausa

p		2a		3x		p
	*		*		=1 ⇔		=1
q		3a		2x		q

p=q |SC|=SB| cnw =======