Calka
Jula: Obliczyć pole obszaru ograniczonego liniami:
x=−1, y=0, y=arctgx, x=
√3
| | π | | 3ln2 | | √3π | |
Czy wynik to: |
| − |
| + |
| ? |
| | 4 | | 2 | | 3 | |
10 lut 23:26
chichi:
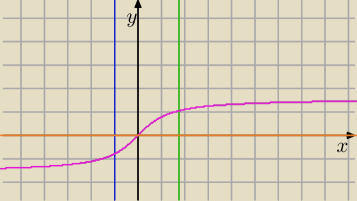
11 lut 00:11
chichi:
Masz taki rysunek?
11 lut 00:12
Min. Edukacji: A skąd ona nie umie rysować tylko kopiuj−wklej
11 lut 08:00
chichi:
A jak żeś to liczyła?
12 lut 02:44
Mariusz:
∫
0√3arctg(x)dx − ∫
−10arctg(x)dx
| | 1 | | 1 | |
xarctg(x)− |
| ln(1+x2)|0√3 − (xarctg(x)− |
| ln(1+x2))|−10 |
| | 2 | | 2 | |
| | 1 | | 1 | |
√3arctg(√3)− |
| ln4−(0−(−1*arctg(−1)− |
| ln2)) |
| | 2 | | 2 | |
| | π | | 1 | |
√3arctg(√3)−ln2−(−( |
| − |
| ln2)) |
| | 4 | | 2 | |
| | π | | 1 | |
√3arctg(√3)−ln2+ |
| − |
| ln2 |
| | 4 | | 2 | |
Czyli wygląda na dobrze policzone
17 lut 18:17
kerajs:
Jak dla mnie, to pokazane obliczenia są błędne, gdyż nie dotyczą obszaru ograniczonego
wszystkimi wskazanymi w treści zadania liniami.
17 lut 19:52
chichi:
Popieram @
kerajs, to jest źle policzone
17 lut 20:11
Min. Edukacji: Julii to już nie interesuje😄
17 lut 21:34
kerajs:
Oby tylko to. Pewnie się okaże, że zadanie zostało prawidłowo rozwiązane, bo autor właśnie o
takim rozwiązaniu myślał, choć coś innego mu się napisało w treści zadania.
17 lut 21:49
Mariusz:
No to kerajs jak wg ciebie ta całka powinna być zapisana ?
18 lut 16:45
Mariusz:
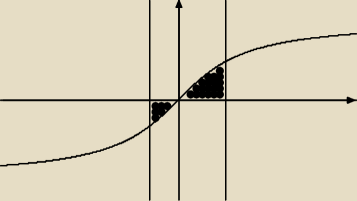
Oto pole jakiego obszaru zostało policzone
Jula zapewne też przeprowadziła te same rachunki
co ja w jednym z poprzednich wpisów
18 lut 18:00
chichi:
No niezbyt to pozostało policzone, znacznie za dużo policzyłeś
18 lut 19:01
chichi:
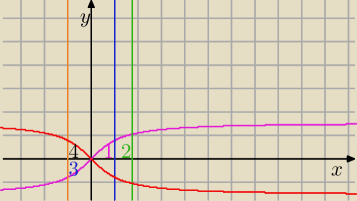
18 lut 19:03
chichi:
Przenalizuj rysunek i zobacz co policzyłeś
18 lut 19:04
chichi:
Cyferki na rysunku oznaczają odpowiednie pola
18 lut 19:04
Mariusz:
No zostało policzone 1 2 3
ale przeczytaj też uważnie wpis z 18 lut 2022 16:45
18 lut 19:21
chichi:
P = 2, bo 3 = −1, Ty policzyłeś 4 + 1 + 2, ale 4 = 1, zatem policzyłeś 2*1 + 2
18 lut 19:24
Mariusz:
A zgadza się 4+1+2 ale to dlatego że nie liczyłem wartości
Gdybym liczył całkę oznaczoną a nie wartość pola obszaru to pewnie bym liczył
tak jak proponujesz
18 lut 19:34
Mariusz:
Gdyby liczyć zgodnie ze wzorem to na przedziale (0,√3)
mielibyśmy całkę z różnicy arctg(x) − 0
a na przedziale (−1,0) mielibyśmy całkę z różnicy 0−arctg(x)
i pole obszaru byłoby sumą pól tych obszarów
18 lut 20:03
kerajs:
''Mariusz: No to kerajs jak wg ciebie ta całka powinna być zapisana ?''
Nijak. Nie ma tu pola ograniczonego przez cztery podane linie, więc i nie ma co liczyć.
19 lut 08:33
Mariusz:
A w ten sposób rozumujesz
Tutaj mamy obszar ograniczony krzywą y=arctg(x) oraz liniami y=0 , x=−1,x=0
oraz obszar ograniczony krzywą y=arctg(x) oraz liniami y=0,x=0,x=√3
i to nie chodziło o te dwa obszary ?
Jula właśnie pola tych obszarów liczyła
Jednego obszaru tutaj nie będzie bo na przedziale <−1,0) arcus tangens
jest ujemny
19 lut 10:14