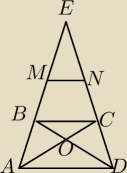pole Loki: W trapezie ABCD (BC < AD) wiadomo, że powierzchnia trójkąta BOC wynosi 9m², a trójkąta AOD 16m² (O to punkt przecięcia przekątnych). Oblicz pole czworoboku AMND jeśli AM = ME, EN = ND i AB∩DC = E.

chichi: Wzorki @Eta Ci pomogą

Loki: Co

Loki: P_ABO=P_COD P_ABO*P_COD=P_BOC*P_AOD ⇒ P_ABO² = 144 P_ABO=P_COD =12

	MA+AD		3MN
PAMND =		*h =		*h = 3PEMN
	2		2

P_MNAD=P_MNBC+49 ale nie widzę dalej związku.

Loki: ok mam wyszło 196/3

an: 6*9=54 a nie 144

	3
P=		(45+6√54)≈66,818
	4

Loki: an a czemu taki wynik?

an: Dlaczego taka wartość o to musisz zapytać twórcę zadania, pokaż jak rozwiązywałeś to zobaczymy dlaczego masz inny wynik.

Loki:

	16		4
Trójkąty OAD i OCB są podobne, ich pola są w stosunku		, a ich boki w stosunku		.
	9		3

	AD
Z kolei trójkaty EAD i EBC są również podobne, więc ich pola są w stosunku (		) 2=
	BC

	16		16		1
		. Dlatego P(EAD)=		*49 . Ponieważ P(EMN)=		P(EAD) mamy, że
	9		9		4

	3		16		196
P(AMND)=		*		*49=
	4		9		3

an: przepraszam ja zamiast 16 wziąłem 6, ale twój wynik jest zły na jakiej podstawie przyjmujesz 16/9 AF=CD⇒ ΔABE≈ΔFBD

	3		16
P=		*49		=84
	4		7

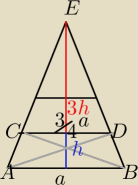an: ΔEAB jest dowolny, trójkąty EAD i EBC będą przystające dla ΔEAB równoramiennego lub różne. Pola ze stosunku, których można wyznaczyć pole ΔEAB przy znanym ABCD na rysunku p/w wyniosą ABE=2ah

	7
ABCD=		ah
	8

Mila:

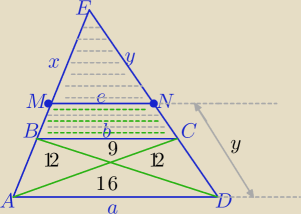
	3		1
b=		a, e=		a, PADCB=49}
	4		2

1) P=P_ΔADE, Ladder theorem

1		1		1		1
	+		=		+
P		16		12+16		16+12

P=112cm² 2)

	1
ΔMNE∼ΔADE w skali k=
	2

	1		112
PΔMNE=		P=		=28
	4		4

4) P_AMND=112−28=84 ================ II sposób P_ΔBCE=S

	3
ΔBCE∼ADE w skali k=
	4

S		9
	=
S+49		16

S=63 P_ΔADE=63+49=112

	1
PΔMNE=		*112=28
	4

P_AMND=112−28=84 ================