Kochana geometria dżemMorelowy:

	3
Środkowe trójkąta o obwodzie d mają długości p, q, r. Wylaż, że p + q + r >		d.
	4

Próbowałam coś tam z twierdzenia kosinusów albo wzoru na długość środkowej, ale nic nie idzie Ktoś ma jakiś pomysł?

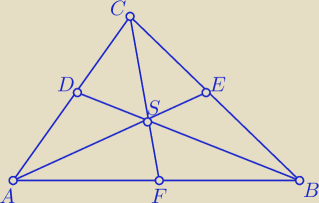chichi: Z ΔABS:

2		2		3
	|AE| +		|BD| > |AB| ⇒ |AE| + |BD| >		|AB|
3		3		2

Analogicznie:

	3		3
Z ΔBSC: |CF| + |BD| >		|BC| oraz z ΔASC: |AE| + |CF| >		|AC|
	2		2

Dodając te trzy nierówności stronami mamy, że:

	3
2(|AE| + |BD| + |CF|) >		(|AB| + |BC| + |AC|)
	2

	3
⇒ |AE| + |BD| + |CF| >		(|AB| + |BC| + |AC|)
	4

□ A Ty jak chcesz, to wstaw sobie swoje literki

dżemMorelowy: Dziekuje!