Geometria analityczna maturaek: Odcinek A'B' gdzie A'(−3;4) i B'(5;6) jest obrazem odcinka AB w jednokładności o środku O(1;2) i skali k≠0. Punkt A leży na prostej y=x−2.Wyznacz pole trójkąta AOB. Mam już prostą A'O y=−¹₂x+⁵₂ oraz punkt A(3,1) Nie wiem jak wyliczyć skalę jednokładności

maturaek: Okej, już wyszła mi k=2 Ale teraz jak obliczyc pole AOB?

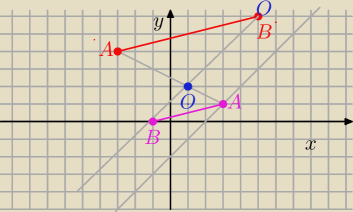
janek191: Oblicz pole Δ A'OB' P_ΔAOB = P_ΔA'OB' : k²

janek191: → OA'= [ −4, 2 ] → OB' = [ 4, 4] więc pole Δ A'OB' jest równe: → → P' = 0,5 I det ( OA', OB' ) I = 0,5*I −4*4 − 2*4 I = 0,5 *24 = 12

maturaek: No i tu kolejny problem, ponieważ wyliczam pole A'OB' i wychodzi mi 60, a w odpowiedzi jest 12. Jak to trzeba zrobić

maturaek: O, dziekuję bardzo. Tak teraz pomyślałam że właśnie wektorami to można rozgryźć