| 3x +4 | ||
Wyznacz zbiór wartości funkcji f(x)= | ||
| x2 + 1 |
| 1 | 1 | |||
ZW=<− | ,4 | > | ||
| 2 | 2 |
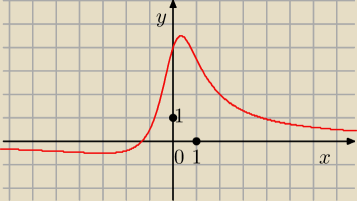
Byłaby, gdyby w mianowniku było 2 x + 1.
| 3x+4 | ||
f(x) = | , Df = R | |
| x2+1 |
| 3−8x−3x2 | ||
f'(x) = | , Df' = Df | |
| (x2+1)2 |
| 3−8x−3x2 | 1 | |||
f'(x) = 0 ⇔ | = 0 ⇔ −(3x−1)(x+3) = 0 ⇔ x ∊ {−3, | } | ||
| (x2+1)2 | 3 |
| 3−8x−3x2 | 1 | |||
f'(x) > 0 ⇔ | > 0 ⇔ −(3x−1)(x+3) > 0 ⇔ x ∊ (−3, | ) | ||
| (x2+1)2 | 3 |
| 3−8x−3x2 | 1 | |||
f'(x) < 0 ⇔ | < 0 ⇔ −(3x−1)(x+3) < 0 ⇔ x ∊ (−∞, −3) ∪ ( | , +∞) | ||
| (x2+1)2 | 3 |
| 1 | ||
Zatem funkcja f posiada minimum lokalne w punkcie x = −3 równe − | , | |
| 2 |
| 1 | 9 | |||
a w punkcie x = | maksimum lokalne równe | |||
| 3 | 2 |
| 1 | 9 | |||
Ponadto lim f(x) = 0, zatem ZWf = [− | , | ]  | ||
| 2 | 2 |
| 3x+4 | ||
f(x)= | , Df=R | |
| x2+1 |
| 3x+4 | ||
f(x)=m ⇔ | =m | |
| x2+1 |
| 1 | 9 | |||
m∊<− | , | > | ||
| 2 | 2 |
| 1 | 1 | |||
ZWf=<− | , 4 | > | ||
| 2 | 2 |
