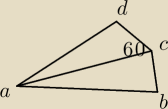
geometria płaska - pola czworokątów Hmmhm: W czworokącie wypukłym ABCD bok DC ma długość 6 oraz |AB|=3|BC|.Przekątna AC ma długość 16 i tworzy z bokiem DC kąt równy 60 stopni. Wiedząc że na czworokącie ABCD mozna opisać okrąg, oblicz pole czworokąta ABCD Mam policzone, że |AD|=14 z twierdzenia cosinusów w trójkącie ACD i pole równe 24√3 Jak mam policzyć pole ABC?

chichi: Tw. Carnota w ΔADC:

	1		1
162 = 62 + 142 − 2 * 14 * 6 * cos(∡ADC) ⇔ cos(∡ADC) = −		⇒ cos(∡ABC) =
	7		7

Tw. Carnota w ΔABC:

	1
162 = (3a)2 + a2 − 2 * 3a * a *		⇒ a = 2√7
	7

Tw. sinusów w ΔADC:

14		16		4√3
	=		⇔ sin(∡ADC) =		= sin(∡ABC)
sin(60o)		sin(∡ADC)		7

	1		4√3
PΔABC =		* 2√7 * 6√7 *		= 24√3
	2		7

Kacper: A czemu nie piszesz twierdzenie Snelliusa, skoro piszesz twierdzenie Carnota?

chichi: Bo mało kto zna tw. sinusów pod nazwą tw. Snelliusa, w przeciwieństwie do tw. Carnota

Hmmhm: Okej, dzięki wielkie!

chichi: I tej nazwy raczej używają fizycy

Kacper: Nie pytałem