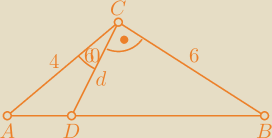
proszę o rozwiązanie anna: dwa boki trójkąta ABC mają długość AC =4 BC = 6 a kąt ACB ma miarę 150⁰ przez wierzchołek C poprowadzono prostą prostopadłą do boku BC która przecięła bok AB w punkcie D oblicz a) długość odcinka CD b) pola trójkątów ADC i CDB

chichi:

	1		1
PΔABC =		*4*6*sin(150o) = 6 ∧ PΔABC =		(4d*sin(60o) + 6d) ⇒ d = 3 − √3
	2		2

	1
PΔACD =		*4*(3 − √3)*sin(60o) = 3√3 − 3
	2

	1
PΔDCB =		*6*(3 − √3) = 9 − 3√3
	2

SPRAWDZENIE: P_ΔACD + P_ΔDCB = 3√3 − 3 + 9 − 3√3 = 6 = P_ΔABC (jest ok)

anna: nie wiem skąd

	1
PΔABC =		(4d*sin(60o) + 6d)
	2

janek191:

	√3
PΔABC =PΔACD + PΔBCD = 0,5*4*d*sin 60o + 0,5*6*d = 2d*		+ 3 d
	2

bo Δ ACD jest prostokątny

janek191: Miało być : Bo ΔBCD jest prostokątny.

anna: dziękuję