| 1 | ||
W trójkącie ABC środkowa BM= | BC. Wykaż że ∡ ABM = ∡BCA + ∡ BAC. | |
| 2 |
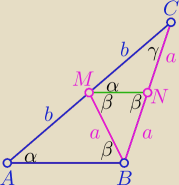 Niech: |∡BAC| = α, |∡ABM| = β, |∡ACB| = γ, ponadto:
MN ∥ AB ⇒ |∡CMN| = α ∧ |∡BMN| = β = |∡MNB|
Z ΔCMN: |∡MNC| = 180o − α − γ ∧ |∡MNC| = 180o − β (kąty przyległe)
⇒ 180o − α − γ = 180o − β ⇒ β = α + γ □
Niech: |∡BAC| = α, |∡ABM| = β, |∡ACB| = γ, ponadto:
MN ∥ AB ⇒ |∡CMN| = α ∧ |∡BMN| = β = |∡MNB|
Z ΔCMN: |∡MNC| = 180o − α − γ ∧ |∡MNC| = 180o − β (kąty przyległe)
⇒ 180o − α − γ = 180o − β ⇒ β = α + γ □ 
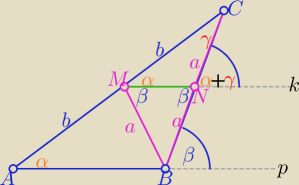 k||p to β=α+γ −− jako kąty odpowiadające
k||p to β=α+γ −− jako kąty odpowiadające







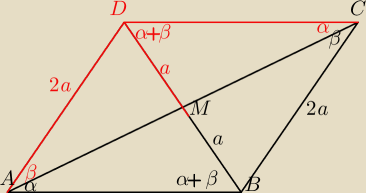 Trójkąt DAB równoramienny, czyli ∡ ABD=∡DAB =∡BCA+∡BAC
Trójkąt DAB równoramienny, czyli ∡ ABD=∡DAB =∡BCA+∡BAC