geometria w R3 wyznacz prosta prostopadlą rybsonn: W przestrzeni R3 3 dany jest punkt A = (2, 5, −7) oraz prosta l : x = 1 + 3t y = 2 − t z = 5t a) Wyznaczyć równanie płaszczyzny π zawierającej prostą l oraz punkt A. b) Znaleźć prostą k prostopadłą do prostej l i zawierającą punkt A. mam problem z podpunktem b, nie umiem kompletnie się za niego zabrać, proszę o pomoc

kerajs: b) wektor kierunkowy tej prostej będzie iloczynem wektorowym wektora kierunkowego prostej l oraz wektora normalnego płaszczyzny π.

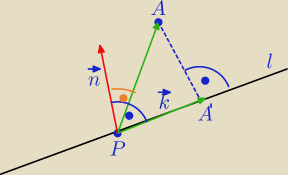
Mila: II sposób b) A = (2, 5, −7) k^→=[3,−1,5]− wektor kierunkowy prostej l A'− Rzut prostopadły punktu A na prostą l. A'=(1+3t,2−t,5t) AA'^→=[3t−1,−t−3,5t+7] [3,−1,5] o [3t−1,−t−3,5t+7]=0 3*(3t−1)+t+3+5(5t+7)=0 t=−1 A'=(−2,3,−5) AA'^→=[−4, −2,2] || [2,1,−1] k₁=[2,1,−1]− wektor kierunkowy prostej m Prosta m⊥l, A∊m x=2+2s y=5+s z=−7−s s∊R