ptoszę o rozwiązanie anna: w układzie współrzędnych umieszczono kwadrat o wierzchołkach A(1,7) B(−7,1) C(−1 , −7) D(7,−1) wyznacz wszystkie wartości parametru a dla których suma odległości wszystkich wierzchołków tego kwadratu od prostej y =ax jest równa 20

anna: jeżeli obliczyłam odległość każdego punktu od tej prostej to suma odległości wynosi zero a nie 20

	4		3
a wynik to a = {−		,		}
	3		4

kerajs: Skoro kwadrat ma bok 10, a wspólnym punktem pęku prostych jest środek kwadratu, to szukane proste będą prostopadłe do dwóch niesąsiadujących boków kwadratu. a=3/4 lub a=−4/3

anna: dziękuję

anna: ponownie mam problem z następującym zadaniem dane są trójkąt o wierzchołkach A(−1,0) B( 1,0) C(0,√3) oraz prosta postaci y = ax+1 Dla jakiego a ∊ <−1, 1> suma d odległości trzech wierzchołków trójkąta ABC od tej prostej jest największa? Wyznacz tę sumę

anna: wynik to a =0 d = 1 + √3

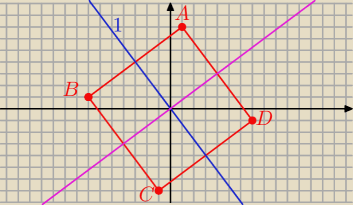
janek191: Mamy 1) y = a x a x − y = 0 I a − 7 I + I − 7a − 1I + I − a + 7 i = I 7a + 1 I = 20 √a² + 1 Dla a ∊ ( − 7, −¹₇) mamy − a + 7 + ( − 7a − 1) = ( − a + 7) + ( − 7a − 1) = 20√a² + 1 12 − 16 a = 20 √a² + 1 / : 4 3 − 4 a = 5 √a² + 1 9 − 24 a + 16 a² = 25 a² + 25 9 a² + 24 a + 16 = 0 Δ = 576 − 576 = 0

	−24		4
a =		= −
	2*9		3

itd.

janek191: W 4 wierszu jest pomyłka − zamiast pierwszej = powinno być +.

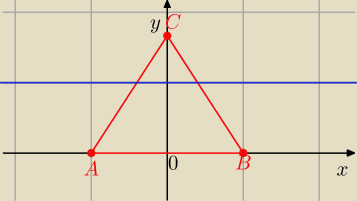
janek191: y = ax + 1 A = ( −1, 0) B = ( 1, 0) C = ( 0, p{3]) a x − y + 1 = 0 I − a + 1 I + I a + 1 I + I − √3 + 1 I = √a² + 1 *d Np. dla − 1 < a < 1 mamy

1 + √3
	= d
√a2 + 1

Dla a = 0 mamy największe d = 1 + √3

anna: dziękuję bardzo