Płaszczyzny Damian#UDM: Zadanie 1. Oblicz odległość punktu P(−2,2,2) od płaszczyzny π przechodzącej przez punkty: A(−5,4,−2) B(1,3,−1) C(−1,2,1) Zadanie 2. Wyznacz punkt Q symetryczny do punktu P(−2,7,−10) względem płaszczyzny π: −x−4y+4z−33=0

Min. Edukacji: https://www.google.com/search?q=odleg%C5%82osc+punktu+od+plaszczyzny&oq=odleg%C5%82osc+punktu+od+plaszczyzny&aqs=chrome..69i57j0i22i30l8.12182j0j8&client=tablet-android-samsung-nf-rev1&sourceid=chrome-mobile&ie=UTF-8

Min. Edukacji: Wystarczy podstawić http://iswiki.if.uj.edu.pl/Odleg%C5%82o%C5%9B%C4%87_punktu_od_p%C5%82aszczyzny a na przyszłość częściej korzystać z podreczników dla Google

Mila: Zadanie 1. 1) Napisz równanie płaszczyzny 2) Skorzystaj z wzoru na odległość punktu od płaszczyzny. Zadanie 2. 1) Znajdź punkt A przebicia z płaszczyzną prostopadłej do płaszczyzny przechodzącej przez P 2) Punkt A jest środkiem PQ Jeśli nie rozwiążesz, to napisz. To łatwe zadania.

Damian#UDM: Jak obliczyć tę macierz, wyznacznik? Mogę odejmować wiersze i kolumny?

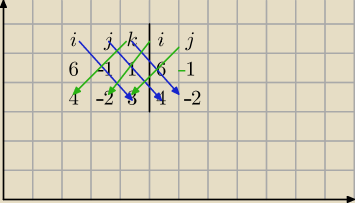
Mila: A(−5,4,−2) B(1,3,−1) C(−1,2,1) AB^→=[6,−1,1] AC^→=[4,−2,3] n^→=[6,−1,1] x [4,−2,3] i j k 6 −1 1 4 −2 3 det(...)=i*(−1)*3+j*1*4+k*6*(−2)−[j*6*3+i*1*(−2)+k*(−1)*4]=−3i+4j−12k−18j+2i+4k=−i−14j−8k n^→=[−1,−14, −8] || [1,14,8] A∊π π: x+5+14(y−4)+8*(z+2)=0 x+14y+8z−35=0 P=(−2,2,2)

	|−2+14*2+8*2−35|		7
d(P,π)=		=
	√1+142+82		√261

Taką masz odpowiedź, czy gdzieś mam błąd rachunkowy?

Damian#UDM: Nieważne z odpowiedzią, bardzo mnie zastanawia jak to zadanie rozwiązać.

Damian#UDM: http://iswiki.if.uj.edu.pl/Odleg%C5%82o%C5%9B%C4%87_punktu_od_p%C5%82aszczyzny tutaj jest macierz 4x4, a Ty Milu użyłaś macierzy 3x3. Nie rozumiem. Naprawdę

Damian#UDM: Zadanie 3. Dane są punkty: A(1,−1,2) B(0,3,−1) C(2,1,1) D(2,3,−2) Oblicz objętość czworościanu rozpiętego na wierzchołkach ABCD. Oblicz odległość punktu A od krawędzi BC. Rozwiązanie 1. Robię trzy wektory wychodzące z jednego wierzchołka. AB^→[−1,4,−3] AC^→[1,2,−1] AD^→[1,4,−4] 2. Obliczam objętość ze wzoru V=¹₆*|(AB^→o(AC^→xAD^→))| V=¹₆* |−1 4 −3| |1 2 −1| = 3 (j³) |1 4 −4| 3. Wektor normalny płaszczyzny BC BC^→=[2,−2,2] Równanie płaszczyzny π:2x−2y+2z+D=0 2*2−2*1+2*1+D=0 → D=−4 π:2x−2y+2z−4=0 Obliczam odległość punktu A od krawędzi BC za wzoru

	|2*1−2*(−1)+2*2|		|2+2+4|		4		4√3
d(A,π)=		=		=		=
	√4+4+4		√12		√3		3

Czy to jest poprawne rozwiązanie?

jc: Odległość A od prostej BC

	|(A−B)x(C−B)|
=
	|C−B|

Damian#UDM: A ten mój sposób? Czy jest ok?

I'm back: Damian, a co to jest "wektor normalny do płaszczyzny BC" jak on powstał? Druga sprawa − nie można wyznaczyć (jednoznacznie) płaszczyzny na podstawie dwóch punktow tejże płaszczyzny Trzecia sprawa − Ty wyznaczyłeś równanie prostej BC, a nie płaszczyzny BC Sposób − yyyyy... powinien być poprawny

Damian#UDM: Dziękuje za wyjaśnienia.