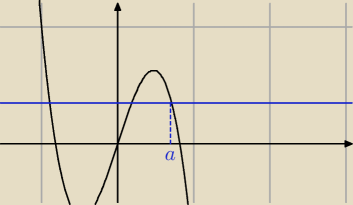
Znajdź liczbę rzeczywistą dla której pola obszarów d1 i d2 były jednakowe Osa: Znajdź liczbę rzeczywistą dla której pola obszarów d1 i d2 były jednakowe, nie wiem jak wstawić zdjęcie, tu jest link https://imgur.com/a/jQ3li5n

kerajs:

	4
Jeśli y=2x−3x3 to postawię na: c=		.
	9

Osa: Czemu akurat taki wynik?

wredulus_pospolitus:

	3		3a4
∫0a (2x−3x3−c) dx = 0 ⇔ [x2 −		x4 − cx]0a = a2 −		− ac = 0
	4		4

dodatkowo wiemy, że: f(a) = c −−−> c = 2a − 3a³ stąd:

	3a4		9a4		4		2
a2 −		− 2a2 + 3a4 = 0 ⇔		= a2 −−−> a2 =		−−−> a =
	4		4		9		3

więc f(2/3) = 4/3 − 3* 8/27 = 4/9 = c stąd