Równanie Pantelejmon: jak rozwiązać takie równanie * xy²+xy−x²? @Mila Czy można do tego podejść tak że np x jest parametrem y zmienną lub y parametrem i x zmienną czyli Δy=x²−4*x*(−x²) = x²−4x³, y1 =..., y2=...? I wtedy się zakłada że delta > 0 ? Tylko że jak narysowałem wykresy tych krzywych w programach graficznych, to wychodzi taki zbiór rozwiązań bez x bo y1 = (....+− √Δ)/ 2a, gdzie a = 2x więc x ≠ 0, natomiast od razu widzimy że x spełnia to równanie. Natomiast jeśli wyznaczymy x1 i x2 to wszystko się zgadza. Jak się wpisze w program graf. to równanie oraz x1 i x2 to suma x1, x2 daje nam wykres (*) lecz suma y1 i y2. I to wygląda tak jakbym zgubił rozwiązanie x = 0, przekształcając równanie (*) wyłączając x przed nawias ... Ale dlaczego gubię to rozwiązanie ? Proszę o wytłumaczenie tego.

janek191: A gdzie tu jest równanie? Mila jest na zdalnym nauczaniu.

Kacper: Napisz równanie, to będziemy mogli pomóc

daras: to forum to tez zdalne nauczanie

janek191: @Daras Tylko zdalne

Mila: rozwiąż równanie: xy²+xy−x²=0 x(y²+y)−x²=0 x(y²+y−x)=0

	1		1
x=0 i y∊R lub y2+y=x⇔ (y+		)2−		=x
	2		4

	1		1
(y+		)2=x+
	2		4

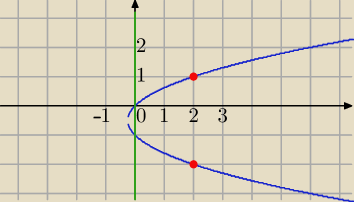
Parabola z poziomą osią symetrii:

	1
x≥−
	4

	1
y+		=±√x+14
	2

	1
y=−		±√x+14
	2

Współrzędne punktów leżących na paraboli spełniają równanie: (y²+y−x)=0 np. dla x=2

	1		9
(y+		)2=
	2		4

	1		3		1		3
y+		=		lub y+		=−
	2		2		2		2

y=1 lub y=−2 (2,1), (2,−2)

Pantelejmon: Rozumiem, dziękuję, a jeszcze odnośnie tego, dlaczego jeśli dla wyjściowego równania policzymy deltę itd. to wtedy to jest błędne bo odrzucamy x = 0 i y ∊ R? bo wtedy x jest w mianowniku y = (−b−√Δy ) / 2a, a = x? Natomiast jeśli liczymy deltę Δx to wszystko się zgadza. ( otrzymamy x₁ i x₂ ) Po prostu dlatego że y ∊ R, a rozwiązaliśmy to wyznaczając y, więc wszystko jest ok? Natomiast wyznaczając Δx = coś z "y", stąd otrzymamy x₁ i x₂ =... i wtedy mamy już uwzględnione rozwiązanie x = 0 bo wyznaczaliśmy "x"?

Pantelejmon: I tutaj można zakładać że Δ > 0 żeby wyznaczyć x₁, x₂ lub y₁, y₂, dziedzina √Δ to co pod pierw. ≥ 0. ewentualnie gdyby nie istniał x₁ x₂, y₁ y₂ tylko x₀ i y₀ to po prostu otrzymamy od razu Δ = 0, tak?