zadania opymalizacyjne, pochodna mk: Dana jest rodzina trójkątów ABC spełniających warunki: A=(−3,5;0); B=(a,0), gdzie a∊(0;4), wierzchołek C należy do paraboli o równaniu y=4x − x² oraz kąt ABC = 90stopni. Wyznacz współrzędne punktu C, dla którego pole trójkąta ABC jest największe. Doszłam do momentu gdzie: IABI=I−3,5−aI IBCI=4a−a²

	I−3,5−aI(4a−a2)
P(a)=
	2

Wiem, że muszę wyznaczyć pochodną, ale nie wiem co mam zrobić z tą wartością bezwzględna. Pomoże ktoś?

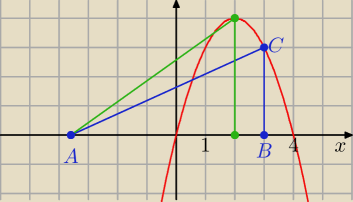
janek191: A =( −3,5 : 0) B = ( a, 0) a ∊ ( 0,4) y = 4 x − x² I AB I = I a − ( −3,5) I = a + 3,5 h = I BC I = 4 a − a² P(a) = 0,5*( a + 3,5)*( 4 a − a²)

ite: dodaję animację: https://www.geogebra.org/geometry/yhbbjksu

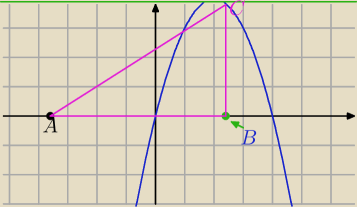
Mila: |−3.5−a|=|a+3.5|=(a+3.5) dla a∊(0,4) 1) P(a)=(a+3.5)(4a−a²) 2)

	1
P'(a)=		(1*(4a−a2)+(a+3.5)*(4−2a))
	2

	−3a2+a+14
P'(a)=
	2

−3a²+a+14=0 Δ=169

	−1−13		7		−1+13
a=		=		lub a=		=−2∉D
	−6		3		−6

napisz jak pochodna zmienia znak dla a∊(0,4) 3)

	1		7		35
B=(2		,0) i C=(		,		)
	3		3		9

Oblicz pole 4)

silnia: Dlaczego h to −a²+4a

wredulus_pospolitus: ponieważ, f(x) = 4x − x² ... podstawiasz x = a i otrzymujesz

chichi: bo jeżeli punkt leży na krzywej, to naturalnie spełnia równanie, które ją opisuje...