pochodne mk: Rozpatrujemy wszystkie trapezy równoramienne, w których krótsza podstawa ma długość 5, i kkażde z ramion też ma długość 5. Oblicz długość dłuższej podstawy tego z rozpatrywanych trapezów, który ma największe pole. Oblicz to pole. Dłuższa podstawa: 5+2x Wysokość: √25−x² zał: xe(0;5)

	(5+5+2x)√25−x2
P=		=(5+x)√25−x2
	2

To wszystko wymnażam i dochodę do wzoru P=√−x⁴−10x³+250x+625 Próbowałam wyliczyć z tego pochodną, ale wyniki wychodzą mi błędne. W internetach widziałam, że ktoś wziął podstawił do wzoru f(x) tylko to co jest pod pierwiastkiem, a potem wyliczył tego pochodną. I wyniki wychodzą dobre. Tylko nie rozumiem dlaczego bierze się tylko to co jest pod pierwiastkiem. Może ktoś wytłumaczyć?

janek191: Pierwiastek jest największy, gdy liczba pod pierwiastkiem jest największa

mk: racja, dzięki

Mila: Nie trzeba włączać (5+x) pod pierwiastek. 1) P(x)=(x+5)*√25−x², x∊(0,5) a=2x+5 2)

	−2x
P'(x)=1*√25−x2+(x+5)*
	2√25−x2

	25−x2+(x+5)*(−x)
P'(x)=
	√25−x2

25−x²−x²−5x=0 −2x²−5x+25=0 Δ=25+2*4*25=225

	5−15		10		5		5+15
x=		=		=		lub x=		=5∉D
	−4		4		2		4

3) a=10 Obliczaj pole.

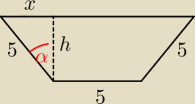wredulus_pospolitus: Trochę inne podejście:

	5+5+2x
Ptrapez =		*h = (5+x)*h = (5+5*sinα)*5cosα = 25(1+sinα)*cosα
	2

f(α) = (1+sinα)*cosα f' = cos²α − (1+sinα)*sinα = cos²α − sin²α − sinα = −2sin²α − sinα + 1

	−1 ± 3
f' = 0 ⇔ 2sin2α + sinα − 1 = 0 −−−> sinα =		−−−> sinα = 1/2 −−−> α = 30o
	4

	75√3
Ptrapez = 25*(1 + 1/2)*√3/2 =
	4

konieczne dodanie odpowiednich komentarzy do obliczeń

wredulus_pospolitus: ach ... no i oczywiście 5+2x = 10