Geometria Analityczna Damian#UDM: 2. Udowodnić, że jeśli x∊R, to |^x+i_x−i|=1. 3. Zapisać w postaci zwiniętej: sin(2x)+sin(4x)+...+sin(2xn). 5. Znaleźć wszystkie rozwiązania równań a) (z+i)⁴=−1 b)z⁶=−i⁶. 11. Znaleźć rzut punktu P(2,3) na prostą o równaniu x−y=1 12. Znaleźć odległość punktu P(2,1,3) od prostej opisanej przez układ równań

	6 −2 −2 6
14. Niech A=		. Oblicz A19.

15. Znaleźć kąt (sinus albo cosinus) między prostymi: l: 2x−3y=1

	⎧	x=2−t
m:	⎩	y=1+t	.

16. Znaleźć objętość ostrosłupa rozpiętego na punktach A(1,−1,0) B(2,0,1) C(0,1,1) D(1,−1,2). 17. Znaleźć odległość między prostymi:

	⎧	x+y−z=2
l:	⎩	y−z=1

	⎧	x=2+t
m:	⎨	y=2t
	⎩	z=−1−t

18. Sprawdzić, czy punkt A(1,2,3) leży na płaszczyźnie opisanej równaniami:

⎧	x=1+t+s
⎨	y=1−t+2s
⎩	z=s

19. Obliczyć odległość punktu A(2,5) od okręgu o równaniu x²+y²+6x−2x+6=0. 20. Obliczyć odległość punktu A(1,0,3) od płaszczyzny P opisanej równaniami:

⎧	x=2−t+s
⎨	y=1+s	.
⎩	z=t

21. Znaleźć równanie stycznej do paraboli y²−x=0 przechodzącej przez punkt A(1,1).

Saizou : Jakieś wkład własny?

Damian#UDM: 11. Schemat rozwiązania: a) Prosta prostopadła do prostej y=x−1 i przechodząca przez punkt P. b) Punkt przecięcia się tych prostych. Czy będzie to poprawne rozwiązanie? 15. Schemat rozwiązania: a) Podstawić pod parametr t dwie wybrane wartości, b) Zapisać równanie prostej w postaci kierunkowej, c) Zapisać równanie prostej l w postaci kierunkowej, d) Skorzystać ze wzorów z tablic na przecięcie się prostych pod takim kątem α, że

	a1−a2
tg(α)=|		|
	1−a1*a2

Czy to rozwiązanie jest poprawne? 19. Schemat rozwiązania: a) Równanie okręgu w postaci kanonicznej, b) Równanie prostej k przechodzącej przez punkt A i środek okręgu S, c) Punkty wspólny prostej k i okręgu, d) Prosta l prostopadła do prostej k i przechodząca przez punkt P wspólny okręgu i prostej k i położony najbliżej punktu A, e) |AP|. Czy ten schemat jest poprawny? 21. Schemat rozwiązania: a) zamiana współrzędnych, b) wyznaczenie stycznej ze wzoru, c) zamiana współrzędnych. Czy ten schemat jest poprawny? I ogólnie to zapraszam do pomagania! Chciałbym, żeby ten wątek był jednym wielkim kompendium wiedzy z poprawnymi rozwiązaniami PROSZĘ O POTWIERDZENIE PRAWDZIWOŚCI POWYŻSZYCH SCHEMATÓW zaproponowanych przeze mnie. Dziękuje Wam, że tu jesteście!

Saizou : 19. d(A,O) = ||AS|− R|, gdzie S− środek okręgu, R − promień okręgu

Damian#UDM: Ja nie wierzę, o wiele szybszy sposób − nie wpadłbym na to − dziękuję!

Saizou : ZAD 2

	x+i		x+i		x2−1+2xi
z =		*		=
	x−i		x+i		x2+1

	x2−1		2x
|z|2 = [Re(x)]2 + [Im(z)]2 = [		]2 + [		]2 =
	(x2+1)		x2+1

x4−2x2+1+4x2		x2+1
	= [		]2 = 1
(x2+1)2		x2+1

|z| = 1

Saizou : Nie wiem co rozumiesz przez postać zwiniętą? ZAD 3 sin(2x)+sin(4x)+...+sin(2xn) = ∑_k=1ⁿ (sin(2k*x)) ZAD 5a (z+i)⁴=−1 (z+i)⁴+1 = 0 (z+i)⁴−(i)² = 0 [(x+i)²−i][(x+i)²+i]=0 dokończ...

Damian#UDM: Zad. 5 a) (z+i)⁴−i²=0 [(z+i)²−i]*[(z+i)²+i]=0 1. (z+i)²−i=0 z²+2iz−1−i=0 Δ_z1=−8+4i=a²−b²+2abi

⎧	a2−b2=−8
⎩	2ab=4

⎧	z1=−4−2√5+(2−√5)i
⎩	z2=2√5−4+(2+√5)i

2. część podobnie. Jest to poprawne rozwiązanie?

Damian#UDM: W Zad. 3. chodzi o to, żeby tych kropek nie było, czyli chyba masz dobrze zrobione Saizou

Damian#UDM: Czyli 5. a) dobrze wykminiłem, dziękuję b) podobnie ze wzorów skróconego mnożenia rozpisać?

luui: Zad 3. S = sin(2x) + sin(4x) + ... + sin(2xn) S = Im(e^2ix + e^4ix + ... + e^2nix)

	e2ix(n+1) − e2ix
S = Im(		)
	e2ix − 1

	e2ix(n+1) − e2ix		e−2ix − 1
S = Im(		.		)
	e2ix − 1		e−2ix − 1

	e2ixn − e2ix(n+1) − e0 + e2ix
S = Im(		)
	e0 − e2ix − e−2ix + 1

	e2ixn − e2ix(n+1) − e0 + e2ix
S = Im(		)
	−(e2ix + e−2ix) + 2

	sin(2xn) − sin(2x(n+1)) + sin(2x)
S =
	−2cos(2x) + 2

Damian#UDM: Gdyby ktoś coś z płaszczyzn ogarniał to byłoby super

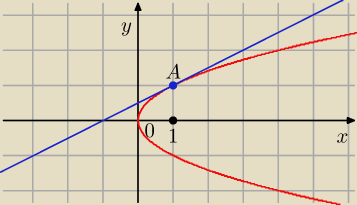
janek191: z.21 y² − x = 0 y² = x y = √x lub y = − √x Styczna w A (1, 1) ma równanie: y = 0,5 x + 0,5 ==============

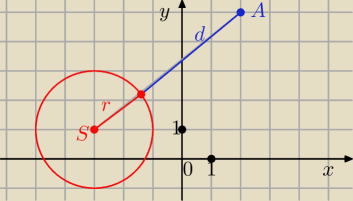
janek191: z.19 A(2, 5) x² + y² + 6 x −2 y + 6 = 0 (x + 3)² + ( y − 1)² = 2² S = ( −3, 1) r = 2 I AS I² = ( −3 −2)² + ( 1 − 5)² = 25 + 16 = 41 I AS I = √41, więc d = I AS I − r = √41 − 2 ===================

Damian#UDM: No to teraz 16, 17, 18 i 20

chichi: A masz odp do 14?

Mila: 16. Znaleźć objętość ostrosłupa rozpiętego na punktach A(1,−1,0) B(2,0,1) C(0,1,1) D(1,−1,2). 1) AB^→=[1,1,1] AC^→=[−1,2,1] AD^→=[0,0,2] 2) 1 1 1 −1 2 1 0 0 2 det(..)=6

	1
V=		*6=1
	6

chichi: Ja postawię na:

	72057731476881408 −72057456598974464 −72057456598974464 72057731476881408
A19 =

Mila: 17) 1) Prosta l: x+y−z=2 y−z=1 równanie parametryczne: z=s, s∊R (1) x+y=2+s y=1+s podstawiam do (1)⇔x=2+s−1−s⇔x=1 ========⇒ l: x=1+0s y=1+s z=s k_l^→=[0,1,1], P₁=(1,1,0)∊l 2) prosta m: x=2+t y=0+2t z=−1−t k_m^→[1,2,−1], P₂=(2,0,−1)∊m 3) proste nie są równoległe: sprawdzamy czy są skośne P₁P₂^→=[1,−1,−1] wyznacznik macierzy: 1 −1 −1 0 1 1 1 2 −1 det(..)=3 − proste są skośne 4) n^→=[0,1,1] x [1,2,−1] =[3,−1,1]−− wektor normalny płaszczyzny równoległej do obu prostych równanie płaszczyzny π: P₁=(1,1,0)∊π 3(x−1)−(y−1)+z=0 3x−y+z−2=0 5) Odległość P₂ =(2,0,−1 od płaszczyzny

	|3*2−0+(−1)−2|		3		3√11
d(P2,π)=		=		=
	√32+1+1		√11		11

Mila: Podaj odpowiedzi do zadań.

Damian#UDM: Dziękuje Wam kochani Zobaczę czy mam i dam Wam znać.