dane są dwa półokręgi o wspólnym środku O\ sabin

dane są dwa półokręgi o wspólnym środku O\ sabin slawek: Zadanie 108. Dane są dwa półokręgi o wspólnym środku O i średnicach odpowiednio AB i CD (punkty A, B, C, D i O są współliniowe). Punkt P leży na wewnętrznym półokręgu, punkt R leży na zewnętrznym półokręgu, punkty O, P i R są współliniowe. Udowodnij, że |<APB| + |<CRD| =180° . sabin:

5 mar 21:17

Eta:

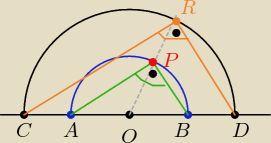
Kąty wpisane oparte na średnicach są kątami prostymi więc | < ABP|= 90^o i |<CRD|= 90^o to: |<APB|+ |<CRD|= 180^o

5 mar 23:55

Jack: Świetny rysunek, jakim programem takie robić? emotka

6 mar 00:11

Eta: Naszym forumowym emotka

kliknąć zakładkę nad polem tekstowym : "rysuję" i wybrać opcję półokręgów . + kolory .

6 mar 00:14

Jack: dzięki... faktycznie: pierwszy raz wszedłem na forum. Genialna opcja! emotka

6 mar 00:17

Eta: Witam nowicjusza emotka

..... i zapraszam do częstych odwiedzin emotka

6 mar 00:18

DiS: to zadanie jest zle zrozumiane emotka

tam gdzie jest C powinno byc A a tam gdzie jest D powinno byc B prosze o pomoc w rozwiazaniu takiego zadania

6 mar 22:08