BADANIE PRZEBIEGU ZMIENNOŚCI FUNKCJI Wiktoria:

	x + 2
f(x)=		Oblicz dziedzinę, asymptoty, monotoniczność i ekstrema,
	(x − 1)2

wklęsłość/wypukłość (BADANIE PRZEBIEGU ZMIENNOŚCI FUNKCJI) Proszę o pomoc z tym zadaniu

chichi: No i gdzie się Panna zacieła?

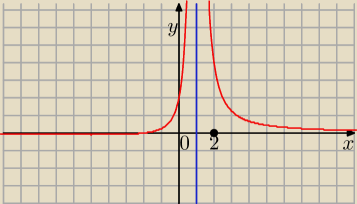
janek191: Dziedzina : x ≠ 1

	x +2
f(x) =
	x2 −2 x+ 1

lim f(x) = +∞ x→ 1⁻ lim f(x) = +∞ x→ 1⁺ Asymptota pionowa: x = 1

janek191:

	1*(x2 −2 x +1) − (x +2)*(2 x − 2)
f '(x) =
	(x2 −2 x +1)2

	− x2 − 4 x +5
f '(x) =
	(x2 −2 x +1)2

Wiktoria: I to wszystko? Na wykładzie miałam jakoś bardziej rozbudowane to i nic nie rozumiałam

janek191: To jest początek

Wiktoria: To co dalej mam liczyć? Bo ja tego w ogóle nie umiem

janek191: f ' (x) =0 ⇔ − ( x + 5)*(x −1) = 0 ⇔ x = − 5 f '(x) < 0 dla x < − 5 lub x > 1 f ' (x) > 0 dla x ∊ ( − 5, 1 ) zatem funkcja f maleje w ( − ∞, − 5) , rośnie w ( − 5, 1) , maleje w ( 1, +∞) f osiąga minimum lokalne w x = − 5.

janek191:

	1 + 2x
lim f(x) = lim		= 0
	x −2 + 1x

x→ −∞ x→ −∞

	1 + 2x
lim f(x) = lim		= 0
	x − 2 + 1x

x→ +∞ x→ +∞ Asymptota pozioma : y = 0

janek191:

	1
y min = f(−5) = −
	12

janek191: Polecam książkę. L. Krysicki. L. Włodarski Analiza matematyczna w zadaniach − tom 1. Rozdział X ( s. 185 − 230) np. Wyd. Naukowe PWN W −wa 2013 r. Jest w pdf.