stereometria Freak: Dany jest ostrosłup prawidłowy trójkątny, w którym krawędzie boczne mają długość b. Kąt płaski ściany bocznej przy wierzchołku ostrosłupa ma miarę 2α. Oblicz objętość ostrosłupa.

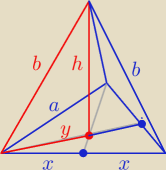
janek191: a = 2 x

	x
sin α =
	b

x = b sin α a = 2b sin α −−−−−−−−−−−−−−−−

	a2 √3
Pp =		= b2 sin2 α
	4

	√3
hp = a*		= √3 b*sin α
	2

	2		2√3
y =		hp =		b*sin α
	3		3

	4		4
h2 = b2 − y2 = b2 −		b2 sin α = b2*( 1 −		sin α)
	3		3

h = b *√( 1 − ⁴₃ sin α)

	1
V =		Pp*h =
	3

janek191: W P_p zgubiłem √3

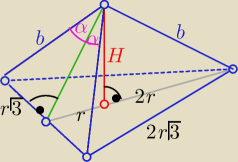Eta: r −− dł. promienia okręgu wpisanego w podstawę P_p=3r²√3 r=bsinα to P_p= √3b²sin²α

	b
H2=b2−4r2 ⇒ ...... H=		√3−4sin2α
	√3

	b3sin2α√3−4sin2α
V=
	3

Freak: Dziękuję wam bardzo, teraz już rozumiem to zadanie