Nierówność kwadratowa z parametrem
Damian#UDM: 14. (0−6)
Wyznacz wszystkie wartości parametru m, dla których przedział (2,3) jest zawarty w zbiorze
rozwiązań nierówności
(m+1)x
2+mx+1<0
Dla Funkcji liniowej
1) m=−1
x>1, czyli (2,3) zawiera się, więc m=−1.
Dla a≠0, m≠−1 mamy funkcję kwadratową
Jak ma być przedział w zbiorze rozwiązań to
Δ>0
I co jeszcze? Myślałem nad
3. k{x
1<2 &x
2>3 4. k{x
1<2 &x
2<2 &x
1<x
2
Z 3. wychodzą cholernie duże liczby, jeśli zakładając, że nie zrobiłem błędu to otrzymałem
m
2−4m−4>(12m
2+31m+14)
2
Ale myślę, że nie warto tego dalej rozwiązywać. Zapraszam do pomagania

27 sty 01:00
Eta:
1/ m=−1
2 / m≠ −1
Δ>0 i f(2)<0 i f(3)<0
27 sty 01:25
chichi:
Jak dla mnie tu będzie dużo więcej przypadków

27 sty 01:36
Eta:
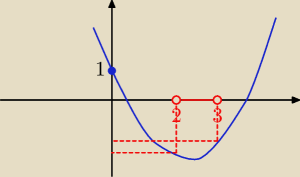
27 sty 01:44
Eta:
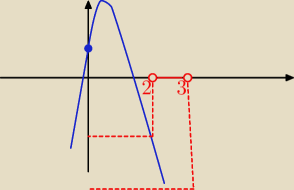
w 2/ też Δ>0 i f)2)<0 i f(3)<0
27 sty 01:49
Damian#UDM: No właśnie narysowałem takie same rysunki pomocnicze le z nie wiedziałem jakie warunki dobrać.
Dziękuję

27 sty 01:58
Eta:
@
chichi
w/g mnie wystarczy,bo 1 na osi rzędnych ogranicza nam pole manewru ..

27 sty 02:04
chichi:
@
Eta rzeczywiście, nie zwracałem zbytnio uwagi na samą postać równania, tylko obrazowałem
sobie w głowie możliwe sytuacje w zależności od współczynnika kwadratowego

Później zerknę jeszcze na to zadanie

27 sty 12:58



 w 2/ też Δ>0 i f)2)<0 i f(3)<0
w 2/ też Δ>0 i f)2)<0 i f(3)<0


 Później zerknę jeszcze na to zadanie
Później zerknę jeszcze na to zadanie 