prośba tet13: Gdzie można znaleźć arkusz − matura próbna z nową era 202 roku.

wredulus_pospolitus: nooo ... maturę z 202 roku będzie ciężko znaleźć

ABC: ja mam ten arkusz 2022 , a także klucz odpowiedzi , co chcesz się dowiedzieć z niego?

daras: łatwiej p.n.e

chichi: @ABC pojawiło się coś ciekawego na rozszerzeniu?

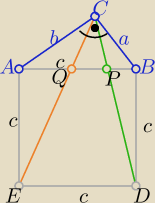
a@b: @chichi Na rozszerzeniu było take zadanie: Wyka,że stosunek pola trapezu DEQP do pola trójkąta PQC

	1		1
jest równy (a2+b2)*(		+		)2
	a		b

chichi: Cześć @Eta, czyli nie postarali się jak zwykle... Łatwe, szybkie i przyjemne P. S. Jak chcesz to wrzucę rozwiązanie

Eta: To wrzucaj Ja też wrzucę po Twoim

chichi: Oki, wrzucę pod wieczór, bo COVID mnie lekko rozłożył...

chichi:

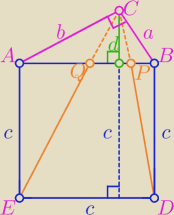
	ab		PΔCED		(d + c)2		c2
ab = cd ⇒ d =		∧		=		= (1 +		)2
	c		PΔCQP		d2		ab

PDEQP		PΔCED − PΔCQP		a2 + b2
	=		= (1 +		)2 − 12 =
PΔCQP		PΔCQP		ab

	1		1
= (a2 + b2)(		+		)2 □
	a		b

chichi: Teraz czekam na Twoje @Eta

daras: szybko wieczór u ciebie, mieszkasz za kołem podbiegunowym?

chichi: Rozmiar buta też chcesz poznać?

Mila: chichi. Zdrowia życzę. Trzymaj się

chichi: @Mila dziękuję kochana, niechaj Ciebie to dziadostwo szerokim łukiem omija!

Mila: Dzięki

Eta:

	PDEQP		c+d
s=		=k2−1 , k=		−−− skala podob.ΔEDC i PQC
	PCQP		d

	ab		c2+2cd
i d=		to k2−1=
	c		d2

	a2+b2
s =(a2+2ab+b2) *
	a2b2

	1		1
s= (		+		)2(a2+b2)
	a		b

Eta: Zdrowia ! chichi

chichi: No to rozwiązaliśmy identycznie , dziękuję Tobie również duuuuużo zdrówka!

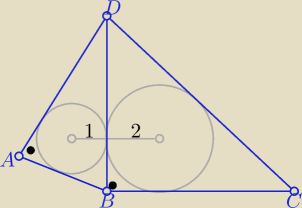
Eta: @chichi 2 zad. z planimetrii na rozszerzeniu było takie: Oblicz obwód czworokąta ABCD

chichi: Ja już w łóżku, ale pokaże rozw. bez większych obliczeń Nic bardziej prostszego: uzupełnić rysunek z tw. o odcinkach stycznych, ponadto zauważmy, że:

3 + 4 − 5
	= 1 (promień okręgu wpisanego w ΔABD)
2

5 + 12 − 13
	(promień okregu wpisanego w ΔDBC)
2

Mamy: L = 4 + 3 + 12 + 13 = 32

chichi:

	5 + 12 − 13
Winno oczywiście być:		= 2
	2

chichi: A jest gdzieś w necie arkusz swoją drogą? Chciałbym zobaczyć resztę zadań

Eta: Arkusza nie ma ale zerknij tu https://www.youtube.com/watch?v=GIZZtPN7CSg

Eta: Niektóre rozwiązania "pokrętne" ( jak dla mnie)

chichi: Dziękuję , wszedłem w pierwsze lepsze zadanie i to był ten dowód, który robiliśmy wyżej. No ten gość z filmiku nieźle popłynął

Eta: No i to jest "piękno planimetrii" Jak już tu kiedyś pisał klasyk: Rozwiązać zadanie każdy może, ale najkrótszą drogą tylko nieliczni mogą............. Dobrej nocki i wstawaj zdrowy !

chichi: Dziękuję i wzajemnie, kolorowych

Eta: W zadaniu z wielomianem też "popłynął " wystarczy rozwiązać układ:

⎧	W(a)=0
⎩	W(−a/2)>a

klasyk: Dojść jakoś do celu potrafi wielu, ale najkrótszą drogą nieliczni mogą. Dla Ety

Eta: ... " i ja mam tę frajdę gdy najkrótszą drogę znajdę "

tet13: arkusz podstawowy

ABC: chcesz arkusz podstawowy w pdf?