nierówności trygonometryczne jan: 2cos²x−9cosx−cosx+4<0 Pierwiastki wyliczone, ale wychodzi mi zły zbiór rozwiązać zamiast np (2kπ;π/3+2kπ)u(5/3π+2kπ;2π+2kπ) wychodzi mi(π/3+2kπ;5/3π+2kπ) . Prosze o pomoc

I'm back: Zacznij od poprawnego zapisu rownania.

jan: Przepraszam równanie to 2cos²−9cosx+4<0

jan: 2cos²x−9cosx+4<0

janek191: cos x = t −1 ≤ t ≤ 1 2 t² − 9 t + 4 < 0 Δ = 81 − 4*2*4 = 49 √Δ = 7

	9− 7
t =		= 0,5 lub t = 4 − odpada
	4

cos x = 0,5

	π		π
x = −		lub x =
	3		3

więc

	π		π
x ∊ ( −		+ 2π*k ,		+ 2π*k) k − dowolna liczba całkowita
	3		3

Jan: A dlaczego bierzemy rozwiązania nad 1/2 a nie pod skoro mamy znak <

Jan: Tz jak narysowakem cosx =1/2 zaznaczyłem te x i wychodzi mi inaczej.

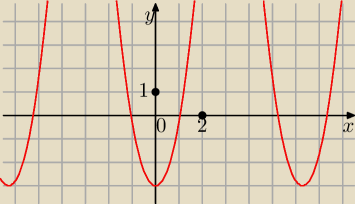
janek191: To jest wykres funkcji y = 2 cos²x − 9*cos x + 4

chichi: Do wszystkich przedmówców − to nie jest równanie.

jan: ja wiem ze to jest brane pod wykres 2cos²x−9cosx+4 ale jest jakis inny sposób który nie opiera się o narysowanie tego wykresu 2cos²x.... ?

jan: Obliczyłem to taki jak mam po to t=1/2 i t=4 ( które wiem że odpadnie) rysuje parabole od 1/2 do 4 i zaznaczam przedział t należy od 1/2 do 4 (bo nierówność jest mniejsza od 0) wychodzę na cos x i pisze że w takim razie cos x.1/2 i cos,4( to odpada) i robię cosx.1/2 czyli szkicuje wykres i szukam dla których x cosx.1/2 znajduje te x i koniec tak mogę?

jan: Obliczyłem to tak: t=1/2 i t=4 ( które wiem że odpadnie) rysuje parabole od 1/2 do 4 i zaznaczam przedział t należy od 1/2 do 4 (bo nierówność jest mniejsza od 0) wychodzę na cos x i pisze że w takim razie cos x>1/2 i cosx<4( to odpada) i robię cosx>1/2 czyli szkicuje wykres i szukam dla których x cosx>1/2 znajduje te x i koniec tak mogę? POPRAWIONE

jan: jednak cosx<4 nie odpada jak napisałem a odpowiedzą są wszystkie liczby rzeczywiste bo co wstawimy za x to i tak cosx będzie mniejszy od 4 Proszę o odpowiedz czy coś jest zle bo też nie wiem czy dobrze myślę