Rysowanie funkcji
Abrakadabra: Jak moge obliczyć zbiór wartości danej funkcji?
| | t | | 1 | | 1 | |
f(x) = |
| przy założeniu t ∊ (− |
| ; |
| ) |
| | 1−2t | | 2 | | 2 | |
20 sty 20:50
chichi:
Zbiorem wartości funkcji będą zbiory jednoelementowe w zależności od tego jakie 't' przyjmiemy
20 sty 20:56
Abrakadabra: No wiem, że metodą podstawiania, ale dlaczego zbiór wartości jako prawidłową odpowiedzią jest:
20 sty 21:01
Fałszywy 6-latek: | | t | |
niechluju matematyczny , ty mówisz o funkcji f(t)= |
| a to wielka różnica |
| | 1−2t | |
na tym forum nie ma edycji więc zanim coś napiszesz 3 razy sprawdź na podgłądzie
20 sty 21:05
chichi:
I w dodatku podaje błędna odpowiedź i mówi, że jest poprawna
20 sty 21:16
Abrakadabra: To znaczy? Co jest nie tak?
20 sty 21:17
Abrakadabra: No nie wiem, akurat jest z książki, tylko chciałem zapytać właśnie dlaczego tak, ale dzięki za
pomóc...
20 sty 21:20
chichi:
To pokaż zdjęcia książki
20 sty 21:25
20 sty 21:32
chichi:
| | t | | t | |
no i tu jest f(t) = |
| , a nie f(x) = |
| |
| | 1−2t | | 1−2t | |
20 sty 21:34
chichi:
poza tym w mianowniku w podręczniku jest +, a nie −
20 sty 21:35
Abrakadabra: Aha no tak, nie zauważyłem, że podałem f(x) xD i tak racja, zapomniałem zamienic na + xd
20 sty 21:38
Abrakadabra: Okej, przepraszam, nie zauważyłem tego, ale nadal nie wiem jak mogę obliczyć Z
w
20 sty 21:43
chichi:
| | 1 | |
Na wykresie nie jest narysowana asymptota pionowa o równaniu t = − |
| do której wykres się |
| | 2 | |
zbliża z prawej strony i tak sobie dąży tam do −
∞ − czyli to jest lewy kraniec naszego zbioru
| | 1 | | 1 | |
wartości funkcji, natomiast prawy należy wyznaczyć licząc f( |
| ) = |
| i wsio |
| | 2 | | 4 | |
20 sty 21:53
Mila:
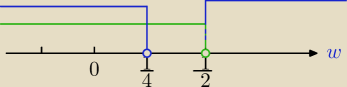
1) Najlepiej wykres i rachunek jak u
chichi
lub
2)
| | t | | 1 | | 1 | |
f(t)= |
| , t∊(− |
| , |
| ) |
| | 1+2t | | 2 | | 2 | |
w− wartość funkcji
t=w+2wt
t−2wt=w
| | 1 | | w | | 1 | | 1 | |
− |
| < |
| < |
| /*2 i w≠ |
| |
| | 2 | | 1−2w | | 2 | | 2 | |
| 2w | | 2w | |
| +1>0 i |
| −1<0 |
| 1−2w | | 1−2w | |
| 2w+1−2w | | 2w−1+2w | |
| >0 i |
| <0 |
| (1−2w) | | 1−2w | |
| 1 | |
| >0 i (4w−1}{1−2w}<0 |
| 1−2w | |
| | 1 | | 1 | | 1 | |
w< |
| i ( w< |
| lub w> |
| )⇔ |
| | 2 | | 4 | | 2 | |
21 sty 16:15
Mila:
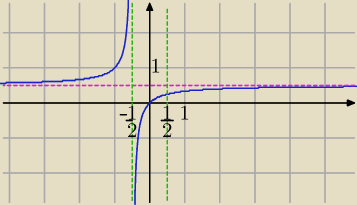
Najlepiej wykres i rachunki jak podał
chichi
21 sty 16:16