proszę o rozwiązanie anna: podstawy trapezu prostokątnego mają długość a i b Wykaż że jeśli w ten trapez można wpisać

	a2 + b2
okrąg to długość dłuższego ramienia jest równa
	a + b

chichi: Nie rozumiem jednego, po co wrzucasz na potęgę te zadnia z geometrii? Cokolwiek się uczysz z tych rozwiązań czy tylko bacznie się im przyglądasz, bo już tyle tego było, a efekt znikomy..

a@b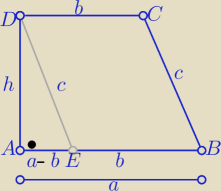: 1/ z warunku wpisania okręgu w trapez h+c=a+b ⇒ h=(a+b)−c to h²= (a+b)²−2(a+b)*c+c² 2/ z tw. Pitagorasa w ΔABE : (a−b)²+h²=c² to (a−b)²+(a+b)²−2(a+b)*c+c²=c² ...................

	a2+b2
c=
	a+b

c.n.w.

chichi: A jak ktoś zna wzór na wysokość trapezu prostokątnego opisanego na okręgu to można tak:

2ab		a2 + b2
	+ c = a + b ⇒ c =
a+b		a+b

a@b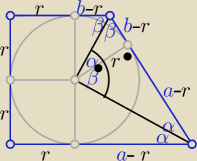: 2 sposób

	ab
r2=(a−r)(b−r) ⇒ r=
	a+b

	2ab
to h=2r=		−− średnia harmoniczna dł. podstaw ( jak podał chichi
	a+b

i h+c=a+b

	2ab
to c= a+b−
	a+b

.......................

	a2+b2
c=
	a+b

==============

chichi: Super , jak się okazuje czasami warto więcej wiedzieć

anna: dziękuję bardzo wszystkim

a@b: Na zdrowie