Całki Podwójne Student Dresiarz: Obliczy a.) ∫∫_D (x²+y²) dxdy, D: x²+y²≤1≤x+y różne wyniki dla kartezjańskiej i biegunowej Kartezjańska wyszła mi π/8 −1/6, Porównując z kalkulatorem wynik dobry, ale sęk w tym, że po rozbiciu na 4 całki tą pierwszą nie umiem obliczyć nie używając wolphram alpha. Podstawienie nie działa a częsci żmudne ∫x²*√1−x²dx. natomiast Biegunowa π/2 − tu przyjąłem dziedzinę uproszczoną x²+y²≤x+y ale chyba błędnie to nie wiem jak to robić. Sugestie Bracia ? b.) ∫∫_D (x+y) dxdy, D: 0≤x , 0≤y, √x+√y≤1 z tym największy problem. Moim zdaniem Dziedzina powala bo sprowadza się do całki niewłaściwej mam wrażenie ale nie znam takich przypadków. Zobaczcie wykres na Geogebrze. Dla biegunowych te pierwiastki to problem

Mariusz: Co do całki ∫x²√1−x²dx to całkowanie przez części działa dobrze Jeżeli chodzi o podstawienie to ∫x²√1−x²dx √1−x² = (1−x)t 1−x² = (1−x)²t² (1−x)(1+x) = (1−x)²t² 1+x = (1−x)t² 1 + x = t² − xt² x + xt² = t² − 1 x(1+t²) = t² − 1

	t2−1
x =
	t2+1

	t2+1−t2+1
√1−x2 = (		)t
	t2+1

	2t
√1−x2 =
	t2+1

	2t(t2+1)−2t(t2−1)
dx =		dt
	(t2+1)2

	4t
dx =		dt
	(t2+1)2

	(t2−1)2	2t	4t
∫				dt
	(t2+1)2	(t2+1)	(t2+1)2

	(t2+1)(t2−1)2		(t2−1)2
=8∫		−8∫		dt
	(t2+1)5		(t2+1)5

	(t2−1)2		(t2−1)2
=8∫		dt−8∫		dt
	(t2+1)4		(t2+1)5

	((t2+1)−2)2		((t2+1)−2)2
=8∫		dt−8∫		dt
	(t2+1)4		(t2+1)5

	(t2+1)2		(t2+1)		1
=8(∫		−4∫		dt+4∫		)dt
	(t2+1)4		(t2+1)4		(t2+1)4

	(t2+1)2		(t2+1)		1
−8(∫		−4∫		dt+4∫		)dt
	(t2+1)5		(t2+1)5		(t2+1)5

	1		1		1
=8(∫		dt−4∫		dt+4∫		dt)
	(t2+1)2		(t2+1)3		(t2+1)4

	1		1		1
−8(∫		dt−4∫		dt+4∫		)
	(t2+1)3		(t2+1)4		(t2+1)5

	1		1		1		1
=8∫		dt−40∫		dt+64∫		dt − 32∫		dt
	(t2+1)2		(t2+1)3		(t2+1)4		(t2+1)5

a na te całki masz wzór redukcyjny

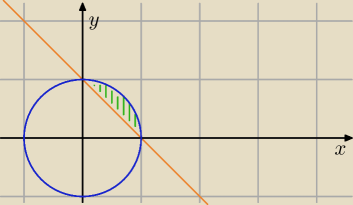
chichi: Co tu upraszczać? Mamy ładny obszar... wyznacz teraz zakres na 'r' oraz na 'φ' i całkuj

Mariusz: ∫∫D (x²+y²) dxdy, D: x²+y²≤1≤x+y Co do tej całki to chyba najtrudniejszym jest poprawne opisanie obszaru po którym całkujemy bo funkcja podcałkowa to r³ (jedno r pochodzi od jakobianu)

Mariusz: chichi " Mamy ładny obszar... wyznacz teraz zakres na 'r' oraz na 'φ' i całkuj " no właśnie najtrudniejsze zostawiłeś dla niego więc wg mnie twoja odpowiedź niewiele mu da

chichi: Ja nie mówię, że zostawiłem prosta rzecz do zrobienia, a jedynie pokazałem jak wygląda obszar, który autor próbował uprościć...

Mariusz: Kąt wygląda na pierwszą ćwiartkę a aby obliczyć jak zmienia się promień trzeba by chyba od promienia okręgu (tutaj jedynka) odjąć promień pochodzący z równania prostej w układzie biegunowym

Mariusz: Ja spadam oglądać na youtube jak gościu programuje rozkład na sumę ułamków prostych Później jeszcze tu wpadnę

Mariusz: Czy obszar można opisać np tak

	π
0≤φ≤
	2

√2
	≤ r ≤ 1
π   2cos(φ− )   4

chichi: Ja mam tak, ale twoja forma jest analogiczna:

	π		1
0 ≤ φ		∧		≤ r ≤ 1
	2		sin(φ) + cos(φ)

I jak się okazuje @Mariusz to była równie banalna część

chichi: A resztę liczy się równie błyskawicznie, niech autor sprawdzi, że wynik będzie zgodny

chichi: A może i nie tak błyskawicznie, zapomniałem że tam funkcje trygonometryczne są w mianowniku

Mariusz: chichi twój rysunek był jednak pomocny choć musiałem się pobawić tym równaniem prostej aby dostać przedział dla r Teraz całkowanie po r jest banalne o ile będziemy pamiętać o jakobianie Całkowanie po φ to najpierw addytywność całki później podstawienie z tym że z podstawieniem trzeba uważać aby je odpowiednio dobrać bo mamy całkę niewłaściwą Co z przykładem b)

Mariusz: a jeszcze jedno mógłbyś napisać dlaczego akurat taki obszar bo na pierwszy rzut oka mogłoby się wydawać jakbyś zmienił zwrot nierówności

chichi: (1) x + y ≥ 1 r(sin(φ) + cos(φ)) ≥ 1

	1
r ≥
	sin(φ) + cos(φ)

(2) r² ≤ 1 r ≤ 1

	1
(1) i (2):		≤ r ≤ 1
	sin(φ) + cos(φ)

Mariusz: Nie , nie z tym to sobie jakoś poradziłem ale chodziło mi o to skąd wziąłeś ten rysunek bo na pierwszy rzut oka to wyglądałoby jakbyś go wykonał dla D: x2+y2≤1≥x+y

Mariusz: a co z przykładem b)

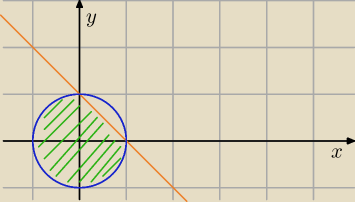
chichi: Rozumiem, rozbijamy na dwie nierówności: (1) x² + y² ≤ 1 − koło o środku w punkcie (0, 0) i promieniu długości równej 1 (2) 1 ≤ x + y ⇔ y ≥ 1 − x − półpłaszczyzna nad prostą o równaniu y = 1 − x My szukamy części wspólnej tych dwóch obszarów, zaznaczyłem go kolorem zielonym

chichi: "D: x2+y2≤1≥x+y" − gdyby było tak wówczas obszar wyglądałby tak: Myślę, że teraz już wszystko jasne

Mariusz: Jeśli chodzi o przedział dla r to robiłem dokładnie tak jak ty tylko na koniec zwinąłem do cosinusa różnicy aby mieć tylko jedną funkcję trygonometryczną

chichi: Ja też później zwinąłem tylko do funkcji sinus, nie cosinus − tutaj dowolnie można:

	π
√2rsin(φ +		) ≥ 1
	4

Mariusz: Dla tego przykładu tak ale jak sobie poradzić np z przykładem b)

chichi: Jeżeli chodzi o (b) to siądę po południu, zaraz lecę na wydział. Hmm może warto się najpierw zastanowić jak wygląda: √x + √y = 1, to akurat będzie proste, wiemy, że musi być: 0 ≤ x ≤ 1 ∧ 0 ≤ y ≤ 1

Mariusz: I tutaj układ kartezjański będzie wygodniejszy ?

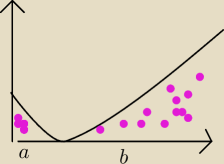
Student D: Rysunek do b.) Ale to 1 i tak jest długie. pomyślcie że student na pwr ma na to tylko 15 minut. A tu jednak myślenie jest a poza tą jedną całką w kartezjańskim , co widać rozbiła się na kolejne 4 całki są jeszcze 3 główne. Skończy się to na liczeniu 16 całek. Więc chyba Biegunka jest tutaj szybsza mam wrażenie. A w tym drugim wykres zapowiada jakby nagle całka podwójna miała by być Sumą Całki Oznaczonej pojedynczej na obszarze a oraz całki niewłaściwej czyli obszaru b.

chichi: Narysuj √x + √y = 1, skąd ty masz ten drugi obszar?

SD: Warunki: x ≥0 i y ≥ 0 i √x + √y ≤1 ⇒ y ≤ (1−√x)² Sprawdź na geogebrze

chichi: Weź dowolne x > 1 a y dowolne takie że y ≥ 0 i co otrzymasz?

chichi: Jak już porządnie wyznaczysz ten obszar całkowanie, nie jak o 13:16 to otrzymasz: ₀∫¹(₀∫^(1−√x)2(x+y)dy)dx =...

Judge: Jak dla mnie to samo co narysował SD

chichi: Nieprawda

Student D: Dalej nie rozumiem. obszar a ok. ale ten b też jest. Wynika z warunków i tego równania y ≤ (1−√x)²

Student D: To dlaczego Geogebra 2D rysuje inaczej

Fafik: Nie lepiej w Biegunowych to zrobić i koniec szopki ?

chichi: "Dalej nie rozumiem. obszar a ok. ale ten b też jest." Przeczytaj moją wypowiedź z 12:34...