Na ile sposobów można rozłożyć 5 kulek w 3 pudełkach
Piotruz: Na ile sposobów można rozłożyć 5 kulek w 3 pudełkach, jeśli każde pudełko musi zawierać co
najmniej jedną kulkę oraz
a) zarówno kulki jak i pudełka są odróżnialne (oznakowane)?
b) kulki są odróżnialne, a pudełka są nieodróżnialne?
c) kulki są nieodróżnialne, a pudełka są odróżnialne?
d) zarówno kulki jak i pudełka są nieodróżnialne?
16 sty 17:39
wredulus_pospolitus:
a) 5! * 4*3
c) 1*4*3
rozumowanie:
Układasz kulki w jedno po drugim. W zależności od tego czy są rozróżnialne czy nie, robisz to
na 5! lub 1 sposób.
Pomiędzy kulkami masz łącznie 4 'przestrzenie' w tych przestrzeniach wkładasz dwie przegrody (w
dwie różne przestrzenie). W zależności od tego czy pudełka są rozróżnialne czy nie, robisz to
Przegrody zaznaczają 'przejście' do następnej pudełka.
16 sty 17:51
Piotruz: Dzięki, szczerze nie kminię za bardzo tej analogii z przegrodami ale daj mi chwilę

16 sty 18:02
wredulus_pospolitus:
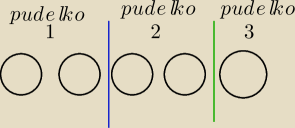
zilustrowanie jednego z podziału
16 sty 18:06
Piotruz: Dobra przegrody oznaczają podział na k− kulka: k k | k | k k , k | k | k k k
czyli jak rozdzielamy kulki po pudełkach. Pierwszy podział w 4 miejscach może być a drugi w 3
więc 4*3 a jak kulki są niezróżnialne to sposobów na wsadzenie po 1 kulce jest 1
16 sty 18:07
Piotruz: O właśnie tak to rozkminiłem jak na obrazku xd
16 sty 18:08
wredulus_pospolitus:
Jednak są to jest złe podejście do tematu ... w końcu 'kolejność kulek' w samym pudełku nie
jest istotna.
16 sty 18:22
wredulus_pospolitus:
Jednak jest to złe ... <−−− tak miało to brzmieć

16 sty 18:22
Piotruz: no niestety ale c i d ogarłem brakuju a i b
16 sty 19:27
wredulus_pospolitus:
przy takiej małej liczbie kulek i pudełek można to zrobić 'na chama':
mamy tylko dwa możliwe układy 3,1,1 lub 2,2,1
a)
1. Wybieramy które pudło ma mieć 3 elementy (3 sposoby)
2. Układamy kule w kolejności (5! sposobów)
3. Dzielimy wynik przez 'kolejność' czyli przez 3!
punkt (2) i (3) to równowartość permutacji z powtórzeniami
+
4. Wybieramy które pudło ma mieć 1 element (3 sposoby)
5. Układamy kule w kolejności (5! sposobów)
6. Dzielimy wynik przez 'kolejność' czyli przez 2!*2!
| | 1 | | 1 | |
czyli mamy: 3*5!*( |
| + |
| ) = ... |
| | 6 | | 4 | |
16 sty 19:39
kerajs:
Mi wychodzi:
c) 3+3=6
d) 2
16 sty 20:37
Piotruz: nie przeanalizowałem b twojego dokładnie ale tobie wynik tam wyszedł 25? mi wychodzi 75 xd
16 sty 20:50
wredulus_pospolitus:
@kerajs ... a co Ty w tym (b) robisz?
mamy bowiem:
123, 4, 5 ; 124, 3, 5 ; 125, 3, 4 ; 134, 2, 5 ; 135, 2, 4
145, 2, 3 ; 234, 1, 5 ; 235, 1, 2 ; 245, 1, 3 ; 345, 1, 2
1, 23, 45 ; 1, 24, 35 ; 1, 25, 34 <−−− *5 (zmieniamy pierwszą cyfrę)
16 sty 21:00
kerajs:
To może pokaż jak dostałeś 75.
Co do pytania wredulusa to widzę w b) zgubiłem 1/2, więc miało być:
co nie zmienia wyniku.
16 sty 21:05
Piotruz: Pytanko jeszcze techniczne o twoje c) u mnie zapisałem to jako 3*2=6. 3+3 w sumie nie rozumiem

A i dlaczego niby 1/2 nie zmienia wyniku


16 sty 21:12
wredulus_pospolitus:
@kerajs −−− teraz się zgodzę

16 sty 21:12
wredulus_pospolitus:
bo podał dobry wynik (25 sposobów), ale zapomniał napisać, że dzieli przez 2 (lewa strona daje
50 a nie 25).
16 sty 21:13
Piotruz: O faktycznie. Dzięki za pomoc!
16 sty 21:17

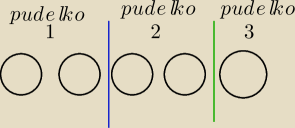 zilustrowanie jednego z podziału
zilustrowanie jednego z podziału

 A i dlaczego niby 1/2 nie zmienia wyniku
A i dlaczego niby 1/2 nie zmienia wyniku

