| 18 | ||
przedłużeniu AC tak, że CE = | Oblicz długość DE | |
| 5. |
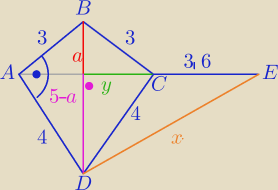 I BD I = 5
y2 + a2 = 9
y2 + ( 5 − a)2 = 16
−−−−−−−−−−−
Odejmujemy stronami
25 − 10 a = 7
10 a = 18
a = 1,8
5 − a = 3,2
y2 = 9 − 1,82 = 9 − 3,24 = 5,76
y = 2,4
więc
x2 = ( 5 − a)2 + ( y + 3,6)2
x2 = 3,22 + 62 = 10,24 + 36 = 46,24
x = 6,8
======
I BD I = 5
y2 + a2 = 9
y2 + ( 5 − a)2 = 16
−−−−−−−−−−−
Odejmujemy stronami
25 − 10 a = 7
10 a = 18
a = 1,8
5 − a = 3,2
y2 = 9 − 1,82 = 9 − 3,24 = 5,76
y = 2,4
więc
x2 = ( 5 − a)2 + ( y + 3,6)2
x2 = 3,22 + 62 = 10,24 + 36 = 46,24
x = 6,8
======
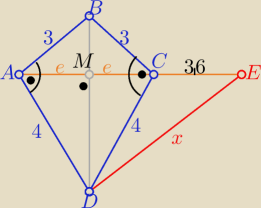
| 3*4 | ||
w ΔABD : |BD|=5 to e= | =2,4 więc |ME|=6 | |
| 5 |