Największa i najmniejsza wartość funkcji w przedziale
julcia: Znajdź największą i najmniejszą wartość funkcji f(x) na podanym przedziale
f(x) = 3√6x2 − x3 x∊[−2,5]
f'(x) = 13(6x2 − x3)−23
13(6x2 − x3)−23 = 0
− x3 + 6x2 = 0
x2(−x + 6) = 0
x = 0 v x = 6
f(0) = 0
f(6) = 0
f(−2) = 3√32
f(−5) = 3√275
Odp. Najmniejsza wartość funkcji to 0. Największa wartość funkcji to 3√275
Czy tak jest dobrze?
16 sty 11:28
chichi:
A dlaczego liczysz f(−5)?

16 sty 11:44
chichi:
I w jaki sposób Ty liczysz w ogóle tę pochodną?

16 sty 11:46
16 sty 11:47
julcia: Faktycznie powinno być f(5) = 3√25
16 sty 11:56
julcia: Obliczanie pochodnej całkowicie zawaliłam, zaraz spróbuję poprawić

16 sty 11:57
julcia: Jak w tym wypadku mam zastosować regułę łańcuchową

16 sty 12:01
chichi:
| | 1 | |
f'(x) = |
| (6x2−x3)−2/3*(12x−3x2) |
| | 3 | |
16 sty 12:05
julcia: Oki, teraz rozumiem
16 sty 12:20
julcia: To teraz rozwiązaniami równania będą liczby 0,6 i 4
f(6) = 0
f(0 = 0
f(4) =
3√32
f(−2) =
3√32
f(−5) =
3√√275
Czyli rozwiązanie się nie zmieni

16 sty 12:26
chichi:
A skąd ta 6 hm?

16 sty 13:06
chichi:
I dlaczego znów liczysz f(−5)...?

16 sty 13:07
ICSP: "To teraz rozwiązaniami równania będą liczby 0,6 i 4"
Tylko x = 4.
Przeczytaj też treść zanim zaczniesz wyznaczać f(6).
16 sty 13:10
julcia: Faktycznie, 6 nie mieści się w przedziale, a 0 podniesione do ujemnej potęgi jest nieokreślone.
Czyli końcowo:
f(4) =
3√32
f(−2) =
3√32
f(5) =
3√275
Najmniejsza wartość:
3√32, największa wartość:
3√275
Dziękuję wszystkim za pomoc

16 sty 13:49
ICSP:
Najmniejsza wartość f(0) = 0
Największa wartość: f(4) = f(−2) = 3√32
16 sty 13:52
janek191:
Oblicz f(5)

16 sty 13:53
julcia: Oj, racja f(5) = 3√25
0 nie mogę podstawić do równania funkcji, prawda?
16 sty 13:58
ICSP: do wzoru funkcji(nie równania funkcji)
Możesz podstawić.
16 sty 14:01
julcia: Oki, dziękuję

16 sty 14:04
janek191:
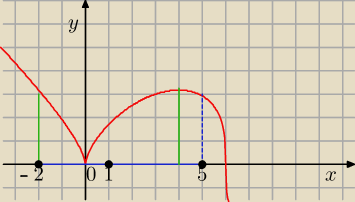
16 sty 14:06










