Przedziały funkcji julcia:

	1
Wyznacz przedziały, na których funkcja f(x) = xln
	x2

jest jednocześnie malejąca i ściśle wklęsła

julcia: Druga pochodna wyszła mi −²_x, ale nie wiem co dalej zrobić

I'm back: Dziwna tą drugą pochodna. Pokaz jak liczysz pochodne

ICSP:

	1
f'(x) = ln(		) − 2
	x2

	2
f''(x) = −
	x

Funkcja malejąca (przedziałami − brak ciągłości w x = 0) f'(x) < 0 Funkcja ściśle wklęsła: f''(x) < 0 Czyli: f'(x) < 0 ∧ f''(x) < 0

julcia:

	1		1		1		1
y'=(xln		) = (x)' * ln		+ x* ( ln		)' = ln		+ x *
	x2		x2		x2		x2

	1		−2		1
		*		= ln		−2
	1x2		x3		x2

	1		1		2		2
y'' = (ln		−2)' = (ln		)' − (2)' = x2 * (−		) = −
	x2		x2		x3		x

julcia: 1. f'(x) < 0

	1
ln		− 2 < 0
	x2

	1
ln		< 2
	x2

1
	< e2 −−> tutaj nie wiem jak dalej do tego podejść
x2

2. f''(x) < 0

−2
	< 0
x

x>0

ICSP:

1
	< e2 // * x2 > 0
x2

x²e² > 1 // :e² > 0

	1
x2 >
	e2

	1
x2 − (		)2 > 0
	e

to jest nierówność kwadratowa. Zastosuj wzór na różnicę kwadratów, następnie narysuj przybliżony wykres i z niego oczytaj rozwiązanie.

julcia: Czyli w 2. x∊(−∞, −¹_e)∪(¹_e, +∞) Łącząc 1 i 2 wychodzi przedział (¹_e, +∞)

ICSP: tak

julcia: Dziękuję Mam jeszcze pytanie do takiego zadania: Wyznacz przedziały, na których funkcja f(x) = 4x + ¹_x jest jednocześnie rosnąca i wypukła. 1.y' = 4 − x⁻²

	1
4 −		> 0
	x2

4x2 − 1
	> 0
x2

x² > ¹₄ x > ¹₂ v x < − ¹₂ x∊ (−∞, −¹₂) ∪ (¹₂, +∞) 2. y'' = (4 − x⁻²)' = 2x⁻³ 2x⁻³ > 0

2
	> 0
x3

x³ > 0 x∊(0, +∞) Łącząc 1 i 2 x∊ (¹₂, +∞) Czy rozwiązanie jest prawidłowe?

julcia:

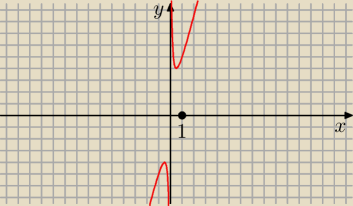
janek191: Wygląda, że tak

julcia: Dziękuję