trójkat Feliks: Dany jest trójkat prostokątny równoramienny, w którym kąt BAC=90^o oraz AB=AC=7. Niech D,E,F będą punktami odpowiednio na bokach BC,CA,AB tak ze kąt EDF=90, DE=5, DF=3. Oblicz długość BD.

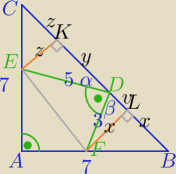
Mila: |EF|=√34, |BC|=7√2 α+β=90^o 1) ΔEKD:

	z		y
sinα=		, cosα=
	5		5

2) ΔFLD:

	x
sinβ=		=sin(90−α)=cosα
	3

	v
cosβ=		=cos(90−α)=sinα
	3

3) Z (1 i 2)

z		v		y		x
	=		,		=
5		3		5		3

4) z+y+v+x=7√2

5		5
	v+		x+v+x=7√2
3		3

8		8
	v+		x=7√2
3		3

	3
v+x=7√2*
	8

	21√3
v+x=
	8

5)

	21√3
|BD|=
	8

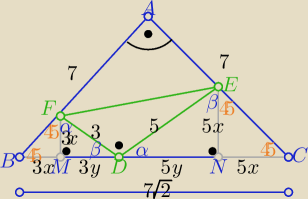a@b: |BC|=7√2

	3
1/ trójkąty DMF i DNE są podobne w skali k=
	5

	|BD|		3x+3y		3		3
2/		=		=		to |BD| =		|BC|
	|DC|		5x+5y		5		8

	21√2
|BD|=
	8

===============