Optymalizacja z wykorzystaniem pochodnej Dżul: Heej, potrzebuje pomocy, rozwiązałam to zadanie, ale bez wykorzystania pochodnej, jak doprowadziłam równanie do najprostszej postaci to wyszedł mi wierzchołek jako minimum, ale niestety muszę użyć tu pochodnej zgodnie z treścią zadania. Wynik: minimalna wartość obwodu 36. Suma długości dwóch boków trójkąta wynosi 24, a miara kąta wewnętrznego zawartego między nimi π3. Wyznacz najmniejszą wartość obwodu tego trójkąta.

PW: Co to jest π3? A skoro już ułożyłeś funkcję na obliczanie obwodu, to ją podaj − sprawdzimy.

wredulus_pospolitus: a,b −−− boki o których mowa w zadaniu a = 24 − b założenia: a > 0 , b>0 , c > 0 (a z powyższego równania mamy: b < 24) z tw. cosinusów: c² = a² + b² − 2ab*cos(π/3) = a² + b² − ab −−−> c = √a² + b² − ab −−−> −−−> c = √ (24−b)² + b² − (24−b)*b obwód: a+b+c = (24−b) + b + c = 24 + c = 24 + √ (24−b)² + b² − (24−b)*b f(b) = 24 + √ (24−b)² + b² − (24−b)*b wyznaczenie pochodnej, a później minimum z takiej funkcji może być troszeczkę problematyczne, więc sobie uprościmy zadanie. zauważamy, że funkcja g(x) = √x jest funkcją monotoniczną, rosnącą (im większy 'x' tym większa wartość), natomiast funkcja h(x) = 24 jest funkcją stałą, zatem więc wiemy, że f(b) = 24 + √ (24−b)² + b² − (24−b)*b osiągnie minimum dla takiego, 'b' dla którego funkcja n(b) = (24−b)² + b² − (24−b)*b osiągnie minimum (przy założeniu: n(b) ≥ 0 ; b>0 ; b<24 ) n'(b) = .... i wyznaczasz minimum

zaq: Okej rozumiem, dziękuję

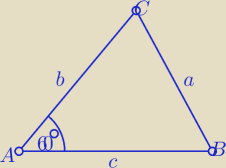
a@b: b+c=24 ⇒ b= 24−c , c∊(0,24) z tw. cosinusów a²=(24−c)²+c²−c(24−c) a²=3c²−72c+576 a −− jest najmniejsze gdy c−−jest najmniejsze

	72
czyli dla odciętej wierzchołka paraboli czyli cmin=		=12
	6

zatem b=24−12=12 więc ΔABC jest równoboczny a=b=c=12 L=36 −− najmniejszy obwód i po ptokach Wredulus "pojechał" na wycieczkę: z Gdańska do Sopotu przez Wrocław

wredulus_pospolitus: @a@b −−− "[...] ale niestety muszę użyć tu pochodnej zgodnie z treścią zadania [...]"

wredulus_pospolitus: PS. Z Gdańska do Sopotu droga już mi się tak znudziła (w końcu z Gdańska jestem ), że musiałem przez Wrocław sobie pojechać (i zobaczyć jak się miasto to zmieniło)

Min. Edukacji: Następnym razem spróbuj przez Bornholm😄