modelowanie student: Dystrybuanta zmiennej losowej X dana jest wzorem: F(x)=0 dla x≤0 1−exp(−3,36x) dla x > 0 Oblicz wartość oczekiwaną zmiennej losowej X. Jak się za to zabrać? Czy 1−exp(−3,36x) nie musi się równać 1?

student: Podobnie tutaj: F(x)=0 dla x≤0

	x
		dla 0 < x ≤ 36
	36

0 dla x > 36 Dlaczego dla x > 36 nie jest 1?

student: Czy w tym drugim to będzie tak?

	x
EX=36*		=x?
	36

wredulus_pospolitus: 1. lim_{x −> +∞} 1 − e^−3.36x = 1 − 0 = 1 2. tak ... winno być 1 dla x>36

wredulus_pospolitus: 3. A w jaki sposób wyznaczamy wartość oczekiwaną mając dystrybuantę ?

wredulus_pospolitus: i co niby oznaczać ma EX = x co to niby jest za wartość oczekiwana?

student: 3. Mając np. taką dystrubuantę: F(x)= 0 dla x≤−3 0.17 dla x∊(−3,4) 1 dla x≥4 No to po prostu bym rozpisał tabelkę z x_i i p_i gdzie x₁ = −3 i p₁ = 0,17 x₂ = 4 i p₂ = 0,83 EX = −3*0,17 + 4*0,83 Dlaczego "w tym drugim" tak nie można, chociaż w sumie skoro jest błąd i winno być 1 dla x>36, to spróbuję Wtedy byłoby:

	x
EX=0*		+1*36 = 36?
	36

wredulus_pospolitus: 18:29 −−− a niby dlaczego Spójrz do teorii EX = ∫_D x*f(x) dx ; gdzie f(x) = F'(x) czyli funkcja gęstości

wredulus_pospolitus: albo szukaj jaki to jest rozkład i sprawdź gotowy wzór na EX

student: To w takim razie czego tyczy się wzór na EX, że ∑_k x_kp_k?

wredulus_pospolitus: no tego samego ... ale w momencie gdy masz dyskretny rozkład ... tutaj z dystrybuanty jak nic widać, że mamy rozkład ciągły a nawet jakbyś się uparł/−a na dyskretnym to nie bierzemy dwóch (brzegowych) wartości tylko WSZYSTKIE

student: "3. Mając np. taką dystrubuantę: F(x)= 0 dla x≤−3 0.17 dla x∊(−3,4) 1 dla x≥4 No to po prostu bym rozpisał tabelkę z xi i pi gdzie x1 = −3 i p1 = 0,17 x2 = 4 i p2 = 0,83 EX = −3*0,17 + 4*0,83 " Czyli to też źle wyliczyłem?

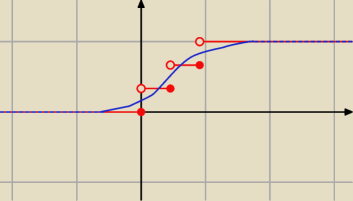
wredulus_pospolitus: Przykład wykresy dystrybuanty dla rozkładu: dyskretnego ciągłego

wredulus_pospolitus: 20:38 −−− nie − tutaj jest dobrze −−− bo tutaj masz rozkład dyskretny (czerwony) masz najpierw wartość 0 ... później jest 'pik' i wartość prawdopodobieństwa zmienia się na 0.17 i jest znowu stała i później znowu masz 'pik' i prawdopodobieństwo zmienia się na 1

student: Masz rację, porąbało mi się totalnie, co nie zmienia faktu, że nie wiem dalej jak to obliczyć, ponieważ potrafię wyznaczyć gęstość dla poszczególnych przedziałów, ale takiego ogólnego wzoru gęstości nie wiem, jak wyznaczyć. F(x)=0 dla x≤0 x dla 0 < x ≤ 36 36 0 dla x > 36 Tutaj gęstość to będzie : f(x)=0 dla x≤0

	1
		dla 0 < x ≤ 36
	36

0 dla x>36

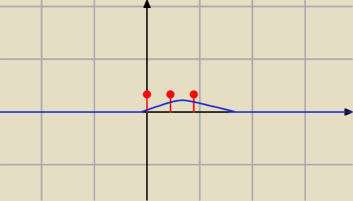
wredulus_pospolitus: o wiele łatwiej zauważyć czy zmienna losowa jest dyskretna czy ciągła z wykresu gęstości: dyskretna ciągła

student: sory, dziwnie się skopiowało. Chodzi o ten przykład z postu drugiego, ten z "exp" na razie zostawmy.

wredulus_pospolitus: no i super i teraz:

	x
∫R x*f(x) dx = ∫−∞0 x*0 dx + ∫036		dx + ∫36+∞ x*0 dx =
	36

	x		x2		362		02		36
= ∫036		dx = [		]036 =		−		=		= 18
	36		72		72		18		2

Co oczywiście odpowiada wzorowi na EX dla rozkładu jednostajnego ciągłego: https://pl.wikipedia.org/wiki/Rozk%C5%82ad_jednostajny_ci%C4%85g%C5%82y gdzie a = 0 ; b = 36

wredulus_pospolitus: Mam nadzieję, że to Ci rozjaśnia sprawę wyznaczania wartości oczekiwanej przy ciągłym rozkładzie prawdopodobieństwa

student : Hm, czyli to jest coś w stylu wyznaczania funkcji dystrybuanty mając gęstość, tyle że przy EX mnożymy nasza funkcja jeszcze przez x?

wredulus_pospolitus: no nieeee .... w przypadku jednostajnej akurat tak, ale już mając ten drugi rozkład to całeczka będzie z goła inaczej wyglądać

wredulus_pospolitus: dopiero teraz doczytałem ... w sumie to tak. Dlatego też −−− raczej się operuje na wykresie (funkcji) gęstości, a nie dystrybuanty. Sam wykres dystrybuanty może być często mylący dla postronnego (niewprawionego) obserwującego.

student : Dzięki, a jak się uporać z tym przykładem wyjściowym z exp?

wredulus_pospolitus: F(x) = 1 − e^−3.36x (olewam zerowy przedział) f(x) = F'(x) = 3.36e^−3.36x więc mamy:

	e−3.36x
3.36 ∫ x*e−3.36x dx = −x*e−3.36x −
	3.36

zauważ, że: ∫ x*e^ax dx = // przez części: u = x ; v' = e^ax

	eax
u' = 1 ; v =
	a

	xeax		eax		xeax		eax
// =		− ∫		dx =		−		czyż nie
	a		a		a		a2

student : Czyli nie obliczymy w tym przypadku „konkretnej” liczby?

wredulus_pospolitus: heee nie ... obliczamy ... po prostu ja Ci policzyłem całkę NIEOZNACZONĄ ... podstawiasz granice całkowania zamiast +∞ wstawiasz lim_x−>+∞ i liczysz

wredulus_pospolitus: granicę 'ze szpitala' będzie najszybciej policzyć