monotoniczność funkcji, pochodne
mk: Wyznacz przedziały monotoniczności funkcji:
Mam problem z tym jak dalej to zrobić. Jak będzie wyglądał taki wykres pochodnej?
| | −1 | |
I jak rozwiązać nierówność: |
| >0? |
| | (x2−4)2 | |
7 sty 12:01
wredulus_pospolitus:
błędnie policzona pochodna
brak pochodnej wnętrza

7 sty 12:09
PW:
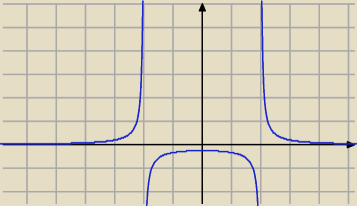
A jeżeli nie było wyraźnego polecenia, by użyć pochodnej, to po co strzelać z armaty do muchy?
g(x) = x
2 − 4
jest ujemna i rosnąca na przedziale [0, 2) oraz dodatnia i rosnąca na przedziale (2, +), a więc
jest na tych przedziałach malejąca (znane twierdzenie).
Podobnie dla przedziałów (−, −2) oraz (−2, 0).
7 sty 13:16
PW: Symbole '∞' mi się zgubiły w zapisach przedziałów.
7 sty 13:17
mk: PW Jak przekształciłes/łaś funkcje f(x)? Mógłbyś pokazać jak to robić krok po kroku?
Robiłam z pochodnej, bo to zadanie było w dziale z pochodnymi.
8 sty 08:13
PW: Nic nie przekształcałem, po prostu oznaczyłem g(x) = x
2 − 4, a zatem badana funkcja
jest odwrotnością funkcji rosnącej i ujemnej na przedziale [0, 2). Jest łatwe do udowodnienia
twierdzenie, że w takim wypadku f jest funkcją malejącą.
Podobnie rozumujemy na pozostałych trzech przedziałach, jak to ilustruje wykres.
10 sty 15:32

 A jeżeli nie było wyraźnego polecenia, by użyć pochodnej, to po co strzelać z armaty do muchy?
g(x) = x2 − 4
jest ujemna i rosnąca na przedziale [0, 2) oraz dodatnia i rosnąca na przedziale (2, +), a więc
A jeżeli nie było wyraźnego polecenia, by użyć pochodnej, to po co strzelać z armaty do muchy?
g(x) = x2 − 4
jest ujemna i rosnąca na przedziale [0, 2) oraz dodatnia i rosnąca na przedziale (2, +), a więc