Trygonometria Iorip: Rozwiąż równanie √3*sin2x+3sinx = 0 , gdzie x∊(0,π). Podaj najmniejsze możliwe spełniające warunki zadania, a także, podaj największe możliwe spełniające warunki zadania. Moje próby rozwiązania zadania wyglądały następująco: √3*2sinxcosx + 3sinx = 0 2√3*sinx*cosx+3sinx = 0 sinx(2√3*cosx+3) = 0 sinx = 0 2√3cosx = −3

	3
cosx = −
	2√3

	√3
cosx = −
	2

Jednak jedyne wyniki jakie mi wyszły to: x = kπ x = π + kπ

	5
x =		π + kπ
	6

	7
x =		π + kπ
	6

	5
Z moich obliczeń wychodzi, że tylko x =		π + kπ, należy do x∊(0,π).
	6

Gdzie w takim razie popełniam błąd? Z treści zadania wynika przecież, że będą dwa wyniki najmniejszy i największy, a ja mam tylko 1. Z góry dziękuje za każdą pomoc.

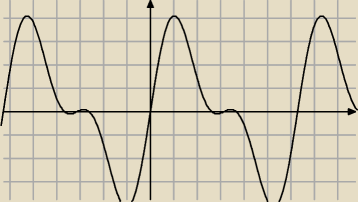
Kacper: W przedziale otwartym to równanie ma tylko 1 rozwiązanie.

chichi: A po co nick zmieniasz?

Iorip: Podczas dodawania zadania nie miałem wyświetlonego poprzedniego nicku, więc wymyśliłem coś na szybko żeby po prostu post dodać, ale miło że ty pamiętasz xD

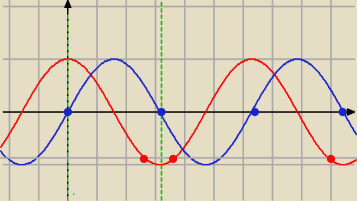
Saizou : gdy rozwiązujesz równanie

	√3
cosx = −		masz rozwiązania
	2

	5
x =		π + 2kπ
	6

	7
x =		π +2kπ
	6

sinx=0 x = kπ (opcja x = π+kπ = π(1+k) = πn, czyli ta opcja pokrywa się) w przedziale (0, π) masz rozwiązania

	5
x =		π,
	6