Relacja czy jest funkcją
anonim123: Jak sprawdzić czy relacje z podpunktu a i d są funkcjami?
4 sty 22:10
a7: nie wkleiłaś zapodaja
4 sty 22:15
4 sty 22:25
a7: e/a) nie jest chyba funkcją, gdyż jest to równanie okręgu (x−2)2+y2=5
4 sty 22:35
4 sty 22:37
a7: (ale może ktoś jeszcze bardziej fachowo odpowie)

4 sty 22:39
anonim123: W poleceniu jeszcze było żeby to uzasadnić to chyba trzeba podać kontrprzykład u😅
4 sty 22:49
a7:
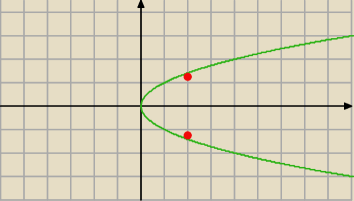
no w obydwu podpunktach dla tych samych iksów występuje więcej niż jedna wartość y
4 sty 23:00
a7: co przeczy definicji czym jest funkcja
4 sty 23:00
a7:
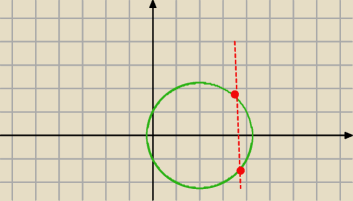
4 sty 23:18
anonim123: http://smurf.mimuw.edu.pl/node/598 A to chyba trzeba skorzystać z tych własności znaleść
takie pary liczb x i y a potem x i z czyli podać kontrprzykład podać jakieś liczby które tego
nie spełniają
5 sty 10:00
anonim123: Mój problem polega na tym że :
Nie bardzo wiem na co wpływa w podpunkcie a) to że xRy a w d) R jest podzbiorem R2?
5 sty 10:01
anonim123: Może ktoś odpowiedzieć na pytanie z 10:01?
5 sty 10:53
a7: może jeszcze ktoś zabierze głos, bo ja odpowiedziałam na poziomie LO
5 sty 13:14
PW: Pytanie z 10:01 to zwykła rozterka początkujących. Kretyni bez wyczucia dydaktycznego potrafią
w jednym zadaniu oznaczać symbolem 'R' jakąś relację (stąd xRy) i jednocześnie dla nich 'R'
to oznaczenie zbioru liczb rzeczywistych.
Stąd takie kuriozalne zapisy jak
R jest podzbiorem R2.
Biedny student ma się domyślić, że to pierwsze 'R' oznacza relację, a jej dziedziną jest R2,
czyli zbiór par liczb rzeczywistych.
Pewnie nie ma już innych liter.
5 sty 13:29
anonim123: A czym różni się rozwiązanie tych zadań od takich z samym R
2 ktoś może rozwiązać?

5 sty 13:42
PW: Wypowiadaj się jaśniej, a najlepiej byłoby przepisać tutaj zadanie.
Nie będę korzystał z zapodaja, bo zasypią mnie reklamami w stylu
− Boli cię kręgosłup od długiego siedzenia przed komputerem? − Kup nasz rewelacyjny gorset.
5 sty 14:02
anonim123: mam dwa przykłady
a)R zawiera się w R
2,xRy wtedy i tylko wtedy gdy x
2−4x+y
2=1
b)R zawiera się w R
2,(x,y) należy do R wtedy i tylko wtedy gdy y
2−x=0
i nie wiem dalej jak je zrobić

5 sty 14:07
anonim123: i mam sprawdzić i udowodnić czy relacja jest funkcją czy nią nie jest
5 sty 14:15
ite: Na zdjęciu z niezawodnego zapodaja widzę (oprócz reklamy gorsetu i nie tylko 🎩👢👙🩳)
zapis, który został przepisany z błędami do zeszytu oraz tu na forum:
a/ R⊂ℛ2, xRy ⇔ gdy x2−4x+y2=1
b/ R⊂ℛ2, (x,y)⊂R ⇔ y2−x=0
Błędy wyglądają na popełnione osoby przepisujące a nie tego, kto to podyktował.
5 sty 14:40
PW: a) Podajemy kontrprzykład:
3R(−2) i 3R2,
(dla pewności można to pokazać podstawiając pary (3, −2) oraz (3, 2) do równania definiującego
relację)
a więc R nie jest funkcją.
5 sty 14:47
anonim123: A dokładniej jak zrobić podpunkt a)?
5 sty 14:53
PW: Podanie kontrprzykładu to jest dowód, że R nie jest funkcją. Nic więcej nie potrzeba,
wystarczy jeden przykład "na nie".
Można oczywiście poszukać wszystkich 'x', które mają dwóch różnych "partnerów" w relacji, ale
po co? Nie pytali o to i szkoda czasu.
5 sty 14:59
anonim123: tylko nie bardzo wiem jak to podstawić?
5 sty 15:01
PW: Masz równanie
x2 − 4x + y2 = 1
i podstawiasz parę (3, −2):
32 − 4.3 + (−2)2 = 1
− zdanie prawdziwe, a więc 3R(−2);
podstawiasz parę (3, 2)
32 − 4.3 + 22 = 1
− zdanie prawdziwe, a więc 3R2.
Skąd akurat (3, 2) i (3, −2)? To kwestia wprawy w rachunkach (kandydat na matematyka w pamięci
robi takie podstawienia i metodą prób i błędów odkrywa takie pary, albo bada kiedy równanie
y2 = − x2 +4x +1
ma prawą stronę dodatnią, a więc rozwiązania są dwa:
y1 = − √−x2 + 4x +1 lub y2 = √−x2 + 4x +1.
Dostanie wtedy nieskończenie wiele "kontrprzykładów".
5 sty 15:12
5 sty 18:05
anonim123: jak podstawiam pod x jedynkę w równaniu na y1 i do y2 jedynkę to ma mi wyjść kontrprzykład?
5 sty 18:13
ite:
na tym ostatnim zapodaju widać zapis jakiejś funkcji na samej górze,
relacja z zad.1 przykład e/ nie jest funkcją,
napisz dokładniej, czego dotyczą pytania z godz.18
5 sty 22:33
anonim123: rzeczywiście pomyliłam się to nie będzie funkcja, ale pytanie z 18:13 jest aktualne

6 sty 14:06
ite: Ja już zupełnie nie wiem, o którą relację pytasz, gdzie podstawiasz, co otrzymujesz, ani co to
jest y
1 i y
2 
.
Kogoś cierpliwszego trzeba do tego wątku (nauczyciele są tu niezastąpieni, choć Min.Edukacji
się z tym nie zgadza).
6 sty 18:19
anonim123: Piszę o poście PW z 15:12
6 sty 18:36
PW: No to jeszcze raz.
Zadanie jest rozwiązane, mamy kontrprzykład : 3R(−2) i 3R(−2). Nic więcej nie potrzeba −
pokazaliśmy w ten sposób, że relacja R nie jest funkcją.
Ponieważ ktoś może wydziwiać − A skąd mam wpaść na takie liczby? − pokazałem sposób znalezienia
wielu takich par.
Równanie definiujące relację R ma postać
(*) y2 = − x2 + 4x +1.
Wiemy, że dla prawej strony Δ = 42 − 4.(−1).1 = 20, √Δ = 2√5, a więc dla x należących
do przedziału
(**) (2 − √5, 2+ √5)
wyrażenie to jest dodatnie (i nie pytaj dlaczego, bo to wie każdy uczeń szkoły średniej). Tak
więc dla 'x' z przedziału (**)
równanie (*) ma dwa rozwiązania wymienione o 15:12.
Jednym z tych 'x' a przedziału (**) jest liczba 3, ale przecie można wziąć dowolną inną, jak
np. 0, i w ten sposób otrzymać inny kontrprzykład:
0R(−1) i 0R1.
6 sty 18:59
PW: Od tego powtarzania w pierwszej linijce wkradł się błąd − powinno być 3R(−2) i 3R2, tak jak w
zapisie z 15:12 dnia 5 stycznia, ale to chyba oczywiste.
Czy już wątpliwości wyjaśnione, czy może opadłaś z sił?
7 sty 12:51
anonim123: Już rozumiem dziękuję 😀
7 sty 20:51
anonim123: jeżeli wyliczę 3R2 i 3R(−2) to skąd wynika że to jest kontrprzykład?
8 sty 16:04
chichi:
Klękajcie narody... Ty w ogóle wiesz czym jest funkcja?

8 sty 16:09
anonim123: przyporządkowanie każdemu x dokładnie jednego y
8 sty 16:26
Maciess:
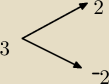
No właśnie! A tutaj, ta domniemana 'funkcja' chce przyporządkować liczbie 3 więcej niż jedną
wartość (przynajmniej dwie z tego co widzę).
Funkcja by nigdy czegoś takie nie zrobiła ( ͡° ͜ʖ ͡°)
Myśle, że najpierw musisz sobie powtórzyć nieco o funkcjach. Polecam książeczkę "Wykłady ze
wstępu do matematyki" pana Guzickiego i Zakrzewskiego.
8 sty 16:58
anonim123: dzięki

8 sty 17:03

 no w obydwu podpunktach dla tych samych iksów występuje więcej niż jedna wartość y
no w obydwu podpunktach dla tych samych iksów występuje więcej niż jedna wartość y




 .
Kogoś cierpliwszego trzeba do tego wątku (nauczyciele są tu niezastąpieni, choć Min.Edukacji
się z tym nie zgadza).
.
Kogoś cierpliwszego trzeba do tego wątku (nauczyciele są tu niezastąpieni, choć Min.Edukacji
się z tym nie zgadza).

 No właśnie! A tutaj, ta domniemana 'funkcja' chce przyporządkować liczbie 3 więcej niż jedną
wartość (przynajmniej dwie z tego co widzę).
Funkcja by nigdy czegoś takie nie zrobiła ( ͡° ͜ʖ ͡°)
Myśle, że najpierw musisz sobie powtórzyć nieco o funkcjach. Polecam książeczkę "Wykłady ze
wstępu do matematyki" pana Guzickiego i Zakrzewskiego.
No właśnie! A tutaj, ta domniemana 'funkcja' chce przyporządkować liczbie 3 więcej niż jedną
wartość (przynajmniej dwie z tego co widzę).
Funkcja by nigdy czegoś takie nie zrobiła ( ͡° ͜ʖ ͡°)
Myśle, że najpierw musisz sobie powtórzyć nieco o funkcjach. Polecam książeczkę "Wykłady ze
wstępu do matematyki" pana Guzickiego i Zakrzewskiego.
