Funkcja kwadratowa, wzory Viete'a
Algorytm: Mając, że
a = m−1
b = −m−1
c = m+1
I mam takie równanie, zrobione za pomocą wzorów Viete'a (jest dobrze zrobione, sprawdzałem w
odpowiedziach):
| (x1+x2)3 − 3x1x2(x1+x2) | |
| < 0 |
| (x1x2)3 | |
| | b | |
Czy da się obliczyć jakoś inaczej to bez podstawiania? (że x1+x2 = − |
| i x1x2 = |
| | a | |
4 sty 20:28
Algorytm: Znaczy, że czy jest jakaś możliwość skrócenia tej ogromnej nierówności? Chciałem skrócić, ale
nie mogę przez parametry

4 sty 20:28
a7: | (m+1)3/(m−1)3−3(m+1)(m−1)*(m+1)/(m−1) | |
| = |
| (m+1)3*(m−1)3 | |
| | (m+1)2(m+1)−3*(m+1)2*(m−1)3 | |
|
| : [(m+1)3)*(m−1)3]= |
| | (m−1)3 | |
=...= 3m
2+6m+4<0
Δ=12
√Δ=2
√3
m
1,2=−3±
√3
m∊(−3−
√3; −3+
√3)
4 sty 20:42
a7: wszystko się ładnie upraszcza (nie wiem czy gdzieś nie ma chochlika wprawdzie) czy rozpisać Ci
bardziej szczegółowo?
4 sty 20:43
Mila:
1)Napisz założenia do mianowników:
2)Wyłącz w liczniku :
(x
1+x
2)
3) Jeżeli podstawisz, to otrzymasz ciekawą postać i nierówność ograniczy się bardzo.
Jeśli tego nie zauważysz to pisz, przedstawię obliczenia.
Podaj odpowiedź, jeśli ją masz w zbiorze.
4 sty 20:44
Algorytm: Znaczy my możemy podzielić przez [(m+1)
3*(m−1)
3]

Bo w założeniu mam, że m nie może być 1, czyli mam dodać jeszcze, że m ≠ −1 również?
4 sty 20:48
a7: no tak
4 sty 20:49
Algorytm: Bo w sumie mogę dodawać do założenia (Bo wcześniej napisałem, analizując, że a ≠ 0, to m − 1 ≠
0, i przez to stwierdziłem, że m ≠ 1)
Czy mogę dodać do założenia dodatkowo, że m ≠ −1, by mogłem skrócić to przez (m+1)3*(m−1)3?
4 sty 20:50
Algorytm: Aha, czyli mogę tak zrobić?
Bo w sumie nie wiedziałem o tym XD
4 sty 20:51
Algorytm: Dziękuję wielkie!
4 sty 20:52
a7: ale zaraz u mnie źle policzone
4 sty 20:53
Algorytm: Aha, no tak XD
Bo ma wyjść, że m ∊ (−1;1)U(1;2)
4 sty 20:59
Algorytm: Dzięki wielkie,
Mila, spróbuje obliczyć

4 sty 21:00
a7: ale u mnie porządnie źle, zaraz poprawie
4 sty 21:00
a7: a, ok
4 sty 21:01
Algorytm: Właśnie próbuję jakoś wykombinować, ale nie udaje mi się xd a7.
Również dzięki wielkie, tylko teraz kombinuje, jak to zrobić xd
4 sty 21:07
a7:
| (m+1)3 | | m+1 | | m+1 | | m+1 | |
| −3* |
| * |
| : [ |
| ]3= |
| (m−1)3 | | m−1 | | m−1 | | m−1) | |
| −2m+4 | |
| <0 dla (uwzględniając dziedzinę czyli m≠1 i m≠−1) m∊(−∞,−1)∪(2,+∞) (?) |
| m+1 | |
4 sty 21:10
a7: mi już wyszło, tylko że co innego niż w Twoich odpowiedziach
4 sty 21:11
Mila:
Inny mam wynik, ciekawa nierówność

4 sty 21:13
a7:
| | (m+1) | | (m+1) | | [ |
| ]2*[ |
| −3] | | | (m−1) | | (m−1) | |
| |
| = |
| |
| | m+1−3m+3 | | −2m+4 | |
= |
| = |
| |
| | m+1 | | m+1 | |
4 sty 21:16
Algorytm: Właśnie mi tak samo wyszło a7, identycznie xd
4 sty 21:16
chichi:
@
Mila sprawdź
20:44 x
1x
2 
4 sty 21:17
a7: a tam na pewno jest <0
4 sty 21:17
4 sty 21:18
Algorytm: Aha, właśnie tu jest napisane, że dana odpowiedź m ∊ (−1;1)U(1;2) uwzględnia w sobie
rozwiązanie warunku 1,
a warunek 1 jest m ≠ 1
4 sty 21:20
a7: jakby tam było > 0 to by się zgadzało z wynikiem w książce, − może literówka?
4 sty 21:20
Algorytm: O Boże, pomyliłem znak XD
4 sty 21:20
Algorytm: Taaaaaaaak, jest > 0 xddddddddddd
4 sty 21:21
Algorytm: Dziękuje wielkie za pomoc!
4 sty 21:21
chichi:
| | b | | c | | m+1 | | m+1 | |
− |
| = |
| = |
| , niech u = |
| , wówczas musimy rozwiązać nierówność: |
| | a | | a | | m−1 | | m−1 | |
| u3−3u2 | |
| < 0 ⇔ u5(u−3) < 0 ⇔ u ∊ (0,3) |
| u3 | |
| | m+1 | |
No, to mamy, że: 0 < |
| < 3 ⇔ m ∊ (− ∞, −1) ∪ (2, + ∞)  |
| | m−1 | |
4 sty 21:23
a7:
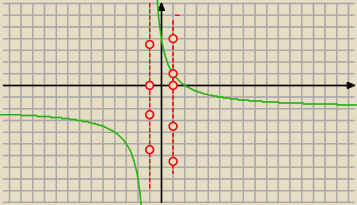
4 sty 21:24
a7: a no to wszystko jasne (20:20)
4 sty 21:25
Algorytm: A kiedy mam dawać w podsumowaniu iloczyn tych rozwiązan, a kiedy sumę?
4 sty 21:26
a7: (21 : 20)
4 sty 21:26
a7: no jak sa założenia to musi być część wspólna z założeniami (założenia trzeba wykluczać z
wyniku) przy rozbijaniu na przypadki czego tu wprawdzie nie było bierze się sumę wyników z
poszczególnych przypadków
4 sty 21:28
a7: założenia trzeba zawsze uwzgledniać w wyniku − to jest nie zawsze takie wykluczanie tylko
właśnie iloczyn− część wspólna wyniku i założeń
4 sty 21:29
Algorytm: | | 5 | |
Właśnie brałem, ale dobrą odpowiedzią jest m ∊ (−1; |
| )\{1} |
| | 3 | |
1 warunek to a ≠ 0, czyli m ≠ 1
| | 5 | |
2 warunek to m ∊ (−1; |
| ) |
| | 3 | |
3 warunek (ostatni) to m ∊ (−1;2)\{1}
Treść zadania jest taka:
Oblicz dla jakiej wartości parametru "m" suma odwrotności sześcianów rożnych pierwiastków
równania (m−1)x
2−(m+1)x+m+1=0 jest dodatnia?
4 sty 21:31
Algorytm: Znaczy brałem sumę tych rozwiązań (Rozwiązania są dobre)
4 sty 21:32
a7: a co wyszło z Δ>0?
4 sty 21:32
Algorytm: to 2 warunek właśnie
4 sty 21:34
4 sty 21:35
a7: no to się zgadza
4 sty 21:36
chichi:
Gdyby było: ma zachodzić to lub to lub to, to byłaby suma, a jeśli ma zachodzić i to i to i to
to jest iloczyn, czy teraz rozumiesz? U ciebie każdy warunek ma zachodzić, czyli musi być
przekrój, wziąłbyś np. 'm' które spełnia np. 2 warunek, a 3 nie, to wówczas nie zachodzi
wszystko co ma zajść

4 sty 21:38
a7:
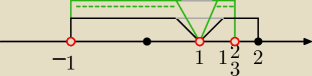
robisz część wspólną wszystkich wyników jakby
4 sty 21:41
a7: w tym zadaniu m musi spełnić naraz wszystkie warunki dlatego część wspólna
4 sty 21:44
Algorytm: Znaczy no wie, czym jest iloczyn tych rozwiązań, tylko jak mam dowiedzieć się, że muszę mieć
sumę, a kiedy iloczyn?
4 sty 21:48
Algorytm:
4 sty 21:48
a7: trzeba wykluczyć 1 oraz −1 bo nie dzielimy przez zero, trzeba wykluczyć liczby spoza przedziału
(−1,5/3 gdyż nie byłoby dwóch rozwiązań równania i na koniec suma odwrotności ma być dodatnia
więc trzeba żeby m było z przedziału (−∞,−1)U(2,∞)
nakładają te trzy warunki naraz mamy prawidłowy wynik
4 sty 21:49
a7: trzeba brać na zdrowy rozsądek
4 sty 21:50
a7: założenia to wykluczenia (jakby) czyli iloczyn (część wspólna)
4 sty 21:51
chichi:
No to tłumaczę Ci, muszą być dwa różne rozwiązania i te rozwiązania muszą spełniać dodatkowo
warunek z polecenia, jak warunków jest kilka, to zawsze bierzemy ich część wspólną, bo biorąc
sumę wziąłbyś wszystkie 'm' dla których równanie miałoby 2 rozwiązania, a nie takie 2
rozwiązania, które spełniają warunek z polecenia... czego tu nie rozumiesz

4 sty 21:51
a7: natomiast w zadaniach, gdzie rozpatrujesz przypadki to w każdym z poszcególnych przypadków
robisz iloczyn a potem sumę
4 sty 21:52
Algorytm: No okej, ale np w zadaniu:
"Dla jakich wartości parametru m dla których funkcja f(x) = (m2 −1)x2 − 2(1−m)x+2 przyjmuje
wartości dodatnie dla każdej liczby rzeczywistej?"
To tam są 2 warunki:
1 warunek to (a > 0 i Δ < 0)
lub
2 warunek to (a=b=0 i c > 0)
Warunek pierwszego rozwiązania to m ∊ (−∞; −3) U(1; +∞)
Warunek drugiego m ∊{1}
A podsumowanie to ich suma m∊(−∞;−3)U<1;+∞)
4 sty 21:53
a7: no bo właśnie są dwa przypadki
4 sty 21:54
Algorytm: Ahaaaaaaaa, już kumam, dzięki!
4 sty 21:54
a7: weź prosty przykład
4 sty 21:55
a7: aa, ok
4 sty 21:55
chichi:
No bo tutaj nie ma mowy o jakichś dwóch różnych rozwiązaniach, tylko o funkcji, nikt nie
zastrzega, że musi być ona f. kwadratową, wówczas rozpatrujemy też przypadek liniowy, a o
przypadkach przed chwilą pisała jako tako @
a7, tak czy inaczej wyłączam się z dyskusji,
bo nie będę uczył bzdurnych schematów jak Ty nie wiesz co jest "pięć"

P.S. Powinni Was w tych szkołach nauczyć chociaż podstaw logiki...
4 sty 21:57
a7: "jako tako" znaczy zrozumiale i bez wywyższania się

4 sty 22:00
Mila:
Najlepiej byłoby, gdyby
Algorytm, podał na początku zadania (1) oryginalną treść zadania.
chichi , zauważyłam błąd, ( tak to jest, gdy trzeba sporo przewijać stronkę)
Podałam 20:44 wskazówkę.
A7 , pisałam, że mam inny wynik niż podałaś 20:42.
Nie włączyłam się do rozwiązania, bo już napisaliście.
Pozdrowienia

4 sty 22:49
a7: z tą oryginalną treścią zadania to tez miałam taką myśl, ale przynajmniej
Algorytm z całą
pewnością wykazuje się własną pracą, a nie czeka na gotowce na co niektórzy się wkurzają
w końcu wyszło

poprawnie
@
Milu ja tam jestem za tym, żebyś się zawsze włączała jeśli tylko masz możliwość, czas,
chęć itp. gdyż wtedy jest "double check" , choćby gdybyś potwierdzała poprawność ostatecznego
wyniku
Pozdrawiam serdecznie

4 sty 22:58

 Bo w założeniu mam, że m nie może być 1, czyli mam dodać jeszcze, że m ≠ −1 również?
Bo w założeniu mam, że m nie może być 1, czyli mam dodać jeszcze, że m ≠ −1 również?






 robisz część wspólną wszystkich wyników jakby
robisz część wspólną wszystkich wyników jakby

 P.S. Powinni Was w tych szkołach nauczyć chociaż podstaw logiki...
P.S. Powinni Was w tych szkołach nauczyć chociaż podstaw logiki...


 poprawnie
@Milu ja tam jestem za tym, żebyś się zawsze włączała jeśli tylko masz możliwość, czas,
chęć itp. gdyż wtedy jest "double check" , choćby gdybyś potwierdzała poprawność ostatecznego
wyniku
Pozdrawiam serdecznie
poprawnie
@Milu ja tam jestem za tym, żebyś się zawsze włączała jeśli tylko masz możliwość, czas,
chęć itp. gdyż wtedy jest "double check" , choćby gdybyś potwierdzała poprawność ostatecznego
wyniku
Pozdrawiam serdecznie 