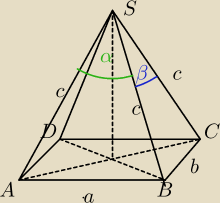
Ostrosłup... etna: Dany ostrosłup ABCDS o podstawie prostokątnej ABCD i krawędziach bocznych długości c. Kąty płaskie w wierzchołku ostrosłupa wynoszą odpowiednio kąt ASB jest równy kątowi CSD=α i kąt BSC jest równy kątowi ASD=β. Oblicz objętość tego ostrosłupa a następnie uzasadnij, że promień okręgu opisanego na trójkącie

	c
ACS wynosi
	√2(cosα+cosB)

a7: z tw cosinusów a=c*√2(1−cosα) b=c*P{2(1−cosβ)} P_p=a*b=2c²√(1−cosα)(1−cosβ) teraz AC=√a²+b² H=c²−AC²/4 V=1/3p_p*H=..

a7: poprawka H=√c²−AC²/4 V=2/3*c³√(1−cosα)(1−cosβ)(cosα+cosβ−1)

a7: nie wiem czy się nie pomyliłam gdzieś w obliczeniach, bo promień wychodzi podobny ale inny niż w treści zadania

Mila: Podaj H .

a7:

	c2(2(1−cosα))+c2(2(1−cosβ)
H=√c2−
	4

Mila: Policzę po 20

a7: ok znalazłam chyba błąd H=c√(cosα+cosβ)/2 V=1/3P_p*H=2/3c³√(1−cosα)(1−cosβ)(cosα+cosβ)/2

	(AC*c2)		c2		c2		c
R=		=		=		=
	(4*1/2AC*H)		2*H		2*c√(cosα+cosβ)/2		√2(cosα+cosβ)

ok wyszło

Mila: d²=2c²*(2−cosα−cosβ)

1		c2*(2−cosα−cosβ)
	d2=
4		2

	1		c2*(2−cosα−cosβ)
(		d)2=
	2		2

	c2*(2−cosα−cosβ)		2c2−2c2+c2(cosα+cosβ)
H2=c2−		=
	2		2

	c2(cosα+cosβ)
H2=
	2

	H2
sin2(ACS)=
	2c2

	(cosα+cosβ)
sin2(ACS)=
	2

	√cosα+cosβ		√2(cosα+cosβ)
sin(ACS)=		=
	√2		2

c
	=2R
√2(cosα+cosβ)   2

	c
R=
	√2(cosα+cosβ)

================