| √5 | ||
płaszczyzny pod kątem α takim, że sinα= | . wyznacz promień podstawy tego stożka | |
| 5 |
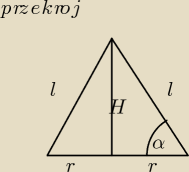 r − szukany promień podstawy
H − wysokość stożka
l − tworząca stożka
Vk = Vs
r − szukany promień podstawy
H − wysokość stożka
l − tworząca stożka
Vk = Vs
| 4 | 4 | 1 | ||||
Vk = | πR3 = | π33 = 36π = Vs = | πr2*H | |||
| 3 | 3 | 3 |
| r | √5 | 5 | ||||
sinα = | = | ⇒ l = r | ||||
| l | 5 | √5 |
| 5 | |
+ cos2α = 1 | |
| 25 |
| 20 | ||
cos2α = | ||
| 25 |
| 2√5 | ||
cosα = | (pomijasz opcję z wartością ujemną, bo to kąt ostry) | |
| 5 |
| H | 2√5 | 2√5 | 2√5 | 5 | ||||||
cosα = | = | ⇒ H = | l = | * | r = 2r | |||||
| l | 5 | 5 | 5 | √5 |
| 1 | 1 | 2 | ||||
Vs = | πr2*H = | πr2*2r = | πr3 = 36π | |||
| 3 | 3 | 3 |